题目内容
17．某几何体的三视图如图所示，则该几何体的体积为（ ）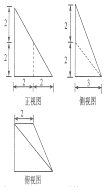
| A． | 8 | B． | 10 | C． | 12 | D． | 14 |
分析 由已知中的三视图，画出几何体的直观图，数形结合可得几何体的体积．
解答 解：由已知中的三视图，可得该几何体的直观图如下所示：
三棱锥A-BCD的体积为：$\frac{1}{3}$×$\frac{1}{2}$×3×4×4=8，
四棱锥C-AFED的体积为：$\frac{1}{3}$×$\frac{1}{2}$×（2+4）×2×3=6，
故组合体的体积V=6+8=14，
故选：D
点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
8．在平面直角坐标系xOy中，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右焦点为F，上顶点为B，M 为线段BF 的中点，若∠MOF=30°，则该椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{1}{3}$ |
5．给出下列四个命题：
①已知m，n是常数，“mn＜0”是“mx2+ny2=1表示双曲线的充分不必要条件”；
②命题p：“?x∈R，sinx≤1”的否定是￢p：“?x0∈R，sinx0＞1”；
③已知命题p和q，若p∨q是假命题，则p与q中必一真一假；
④命题“若a＞b＞0，则a2＞b2”的逆命题是假命题．
其中真命题的序号是（ ）
①已知m，n是常数，“mn＜0”是“mx2+ny2=1表示双曲线的充分不必要条件”；
②命题p：“?x∈R，sinx≤1”的否定是￢p：“?x0∈R，sinx0＞1”；
③已知命题p和q，若p∨q是假命题，则p与q中必一真一假；
④命题“若a＞b＞0，则a2＞b2”的逆命题是假命题．
其中真命题的序号是（ ）
| A． | ①②④ | B． | ①③④ | C． | ②④ | D． | ②③ |
12．已知抛物线C：y2=4x的焦点为F，准线为l，过点F的直线交抛物线于A，B两点（A在第一象限），过点A作准线l的垂线，垂足为E，若∠AFE=60°，则△AFE的面积为（ ）
| A． | $4\sqrt{3}$ | B． | $2\sqrt{3}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |
2．
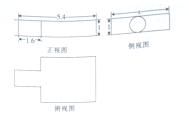中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）| A． | 2.5 | B． | 3 | C． | 3.2 | D． | 4 |
9．在等差数列{an}中，已知a3+a8=6，则3a2+a16的值为（ ）
| A． | 24 | B． | 18 | C． | 16 | D． | 12 |
6．函数$f（x）=-x+\frac{1}{x}$在$[{-2，-\frac{1}{3}}]$上的最大值是（ ）
| A． | $\frac{3}{2}$ | B． | $-\frac{8}{3}$ | C． | -2 | D． | 2 |