题目内容
8.在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,上顶点为B,M 为线段BF 的中点,若∠MOF=30°,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{1}{3}$ |
分析 求出BF的中点M的坐标,利用∠MOF=30°,得到a,b关系,通过a,b,c的关系,求出椭圆的离心率.
解答 解:由题意可知M($\frac{c}{2},\frac{b}{2}$),∵∠MOF=30°,所以tan30°=$\frac{b}{c}$,∴c2=3b2.
又b2=a2-c2,所以4a2=3c2,所以椭圆的离心率为$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查椭圆的基本性质,椭圆的离心率的求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
19.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )
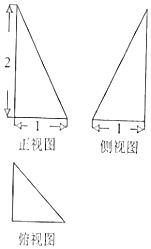

| A. | $\sqrt{6}π$ | B. | 6π | C. | 24π | D. | 36π |
13.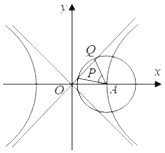 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )
 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点为A,O 为坐标原点,以A 为圆心的圆与双曲线C 的一条渐近线交于 P,Q 两点.若∠PAQ=60°,且|PQ|=$\frac{{\sqrt{3}}}{3}a$,则双曲线C 的渐近线方程为( )| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{2}x$ | C. | y=±3x | D. | $y=±\frac{{2\sqrt{3}}}{3}x$ |
17.某几何体的三视图如图所示,则该几何体的体积为( )
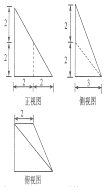

| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
18.求值:$\frac{1-tan15°}{1+tan15°}$=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |