题目内容
已知函数f(x)=ax-1的图象经过点(5,
),其中a>0,a≠1
(1)求a的值;
(2)求函数g(x)=a2x-ax-2+8,x∈[-2,1]的值域.
| 1 |
| 16 |
(1)求a的值;
(2)求函数g(x)=a2x-ax-2+8,x∈[-2,1]的值域.
考点:指数函数的单调性与特殊点,函数的值域
专题:函数的性质及应用
分析:(1)依题意,f(5)=
即可求得a=
;
(2)由于a=
,故g(x)=a2x-ax-2+8=[(
)x-2]2+4,x∈[-2,1],(
)x∈[
,4],利用二次函数的单调性质即可求得g(x)的值域.
| 1 |
| 16 |
| 1 |
| 2 |
(2)由于a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵f(5)=a5-1=a4=
,
∴a=
;
(2)∵a=
,
∴g(x)=a2x-ax-2+8=(
)2x-4•(
)x+8=[(
)x-2]2+4,
∵x∈[-2,1],
∴(
)x∈[
,4],
∴当x=-1,(
)x=2时,g(x)取得最小值,为4;
当x=-2,(
)x=4时,g(x)取得最大值,为8;
∴函数g(x)=a2x-ax-2+8,x∈[-2,1]的值域为[4,8].
| 1 |
| 16 |
∴a=
| 1 |
| 2 |
(2)∵a=
| 1 |
| 2 |
∴g(x)=a2x-ax-2+8=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵x∈[-2,1],
∴(
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=-1,(
| 1 |
| 2 |
当x=-2,(
| 1 |
| 2 |
∴函数g(x)=a2x-ax-2+8,x∈[-2,1]的值域为[4,8].
点评:本题考查指数函数的单调性与特殊点,着重考查指数函数的值域的确定,属于中档题.

练习册系列答案
相关题目
不等式组
表示的平面区域是( )
|
A、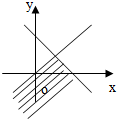 |
B、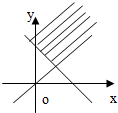 |
C、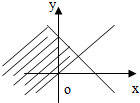 |
D、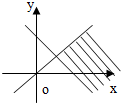 |
函数y=1+4cosx-4sin2x(-
≤x≤
)的值域是( )
| 2π |
| 3 |
| 2π |
| 3 |
| A、[0,8] | ||
| B、[-3,5] | ||
C、[-3,2
| ||
| D、[-4,5] |
如图,已知正方体ABCD-A1B1C1D1中,异面直线AD1与A1C所成的角的大小是( )


| A、30° | B、60° |
| C、90° | D、120° |
 如图,函数f(x)的图象是曲线OAB,其中点O(0,0),A(1,2),B(3,1),则
如图,函数f(x)的图象是曲线OAB,其中点O(0,0),A(1,2),B(3,1),则 如图,四棱柱的底面是菱形,各侧面都是长方形,两个对角面也是长方形,面积分别为Q1,Q.求四棱柱的侧面积.
如图,四棱柱的底面是菱形,各侧面都是长方形,两个对角面也是长方形,面积分别为Q1,Q.求四棱柱的侧面积.