题目内容
正三棱锥的底面积为4
cm2,侧面等腰三角形面积为6cm2,求正三棱锥侧棱.
| 3 |
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:由三角形的面积公式易得底面边长,进而可得斜高,再由勾股定理可得侧棱长.
解答:
解:设正三棱锥的底面边长为a,
∴S=
a2×
=4
,解得a=4,
设正三棱锥的斜高为h,则
×4h=6,
解得h=3,
由勾股定理可得侧棱l=
=
∴S=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设正三棱锥的斜高为h,则
| 1 |
| 2 |
解得h=3,
由勾股定理可得侧棱l=
| 32+22 |
| 13 |
点评:本题考查棱锥的结构特点,涉及勾股定理和三角形的面积公式,属基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
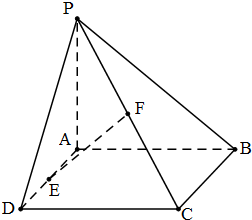 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,