题目内容
((本题15分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M=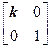 ,N=
,N=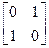 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
(1)求k的值。
(2)判断变换MN是否可逆,如果可逆,求矩阵MN的逆矩阵;如不可逆,说明理由.
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M=
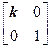 ,N=
,N=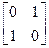 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,(1)求k的值。
(2)判断变换MN是否可逆,如果可逆,求矩阵MN的逆矩阵;如不可逆,说明理由.
解:由题设得 、、、、、、、、、、、、、、、、、、、、4分
、、、、、、、、、、、、、、、、、、、、4分
由 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1( ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是 ,则由题设知:
,则由题设知: 。
。
所以k的值为2或-2。、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、10分
(2)分类讨论、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、15分
 、、、、、、、、、、、、、、、、、、、、4分
、、、、、、、、、、、、、、、、、、、、4分由
 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1( ,-2)。
,-2)。计算得△ABC面积的面积是1,△A1B1C1的面积是
 ,则由题设知:
,则由题设知: 。
。所以k的值为2或-2。、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、10分
(2)分类讨论、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、15分
略

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
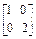 ,N=
,N=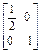 .
. 满足
满足 ,则
,则 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )
个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )




 的
的 逆矩阵;
逆矩阵; ,求
,求
 的参数方程为
的参数方程为 (
( 是参数),曲线
是参数),曲线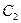 的极坐标方程为
的极坐标方程为 (
( .
. 求曲线
求曲线 (Ⅱ)设曲线
(Ⅱ)设曲线 两点,求弦长
两点,求弦长
 中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( )
中的空白处以构成三行三列方阵,若要求每一行从左到右、每一列从上到下依次增大,则满足要求的填法种数为 ( ) 是线性方程组
是线性方程组 的增广矩阵,则这个线性方程组的解
的增广矩阵,则这个线性方程组的解 可用矩阵表示为 ▲ .
可用矩阵表示为 ▲ . ,该方程组的解为
,该方程组的解为 则
则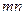
 变换为
变换为 ,则点
,则点 在此变换下所对应的点是
在此变换下所对应的点是