题目内容
4.已知函数$f(x)=\frac{ax}{{{x^2}+1}}(x∈R)$,如图是函数f(x)在[0,+∞)上的图象.(1)求a的值,并判断函数的奇偶性补充作出函数f(x)在(-∞,0)上的图象,说明作图的理由;
(2)根据图象指出(不必证明)函数的单调区间与值域;

分析 (1)由f(1)=$\frac{a}{2}$=2,求得 a的值,可得f(x)的解析式.
(2)结合f(x)的图象可得函数的单调区间以及值域.
解答 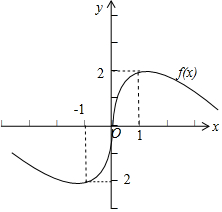 解:(1)由函数$f(x)=\frac{ax}{{{x^2}+1}}(x∈R)$在[0,+∞)上的图象,可得f(1)=$\frac{a}{2}$=2,∴a=4,f(x)=$\frac{4x}{{x}^{2}+1}$.
解:(1)由函数$f(x)=\frac{ax}{{{x^2}+1}}(x∈R)$在[0,+∞)上的图象,可得f(1)=$\frac{a}{2}$=2,∴a=4,f(x)=$\frac{4x}{{x}^{2}+1}$.
由函数的解析式可得f(x)为奇函数,它的图象关于原点对称,
由此可得它在R上的图象.
(2)结合f(x)的图象可得函数的增区间为(-1,1),减区间为(-∞,-1)、(1,+∞).
函数的值域为[-2,2].
点评 本题主要考查奇函数的解析式,函数的奇偶性和单调性的应用,函数的值域,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
15.下列各式正确的是( )
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\root{4}{{a}^{4}}$=a | C. | $\sqrt{{7}^{2}}$=7 | D. | $\root{3}{(-π)^{3}}$=π |
12.一个长方体的棱长分别为1、2、2,它的顶点都在同一个球面上,这个球的体积为( )
| A. | $\frac{9}{4}π$ | B. | $\frac{9}{2}π$ | C. | 18π | D. | 36π |
9.设x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ 4x-y-2≤0\\ x≥0\\ y≥0\end{array}\right.$,则4x•2y的最大值为16.
16.设函数$f(x)={({\frac{1}{2}})^{1+{x^2}}}+\frac{1}{1+|x|}$,则使得f(2x-1)+f(1-2x)<2f(x)成立的x的取值范围是( )
| A. | $({\frac{1}{3},1})$ | B. | $({-∞,\frac{1}{3}})∪({1,+∞})$ | C. | $({-\frac{1}{3},\frac{1}{3}})$ | D. | $({-∞,-\frac{1}{3}})∪({\frac{1}{3},+∞})$ |
10.在区间[0,4]上任取一个实数x,则x>1的概率是( )
| A. | 0.25 | B. | 0.5 | C. | 0.6 | D. | 0.75 |