题目内容
2.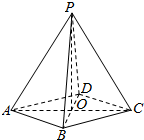 如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.(1)若AC⊥PD,求证:AC⊥平面PBD;
(2)若平面PAC⊥平面ABCD,求证:|PB|=|PD|.
分析 (1)菱形的对角线AC⊥BD,结合已知条件AC⊥PD,利用线面垂直的判定定理可得AC⊥平面PBD;
(2)利用面面垂直的性质定理,结合AC⊥BD得到BD⊥平面PAC,从而BD⊥PO且PO是BD的垂直平分线,得到|PB|=|PD|;
解答 证明:(1)因为底面ABCD是菱形,所以AC⊥BD.
又因为AC⊥PD,PD∩BD=D,
所以AC⊥平面PBD…(4分)
(2)由(1)知AC⊥BD.
因为平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,
BD?平面ABCD,
所以BD⊥平面PAC.
因为PO?平面PAC,
所以BD⊥PO.
因为底面ABCD是菱形,
所以|BO|=|DO|,
所以|PB|=|PD|.…(10分)
点评 本题给出一个特殊四棱锥,要我们证明线面垂直,着重考查了空间平行、垂直位置关系的判断与证明等知识,属于中档题.

练习册系列答案
相关题目
12.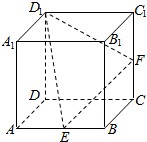 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
①请画出直线l的位置;
②设l∩BC=G,求BG的长.
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,①请画出直线l的位置;
②设l∩BC=G,求BG的长.
17.直线l过点A(2,11),且与点B(-1,2)的距离最远,则直线l的方程为( )
| A. | 3x-y-5=0 | B. | 3x-y+5=0 | C. | x+3y+13=0 | D. | x+3y-35=0 |
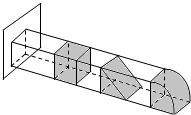 如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.
如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.