题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,已知a:b:c=2:4:5,求
的值.
| 2sinB |
| 3sinC-5sinA |
考点:正弦定理
专题:解三角形
分析:a:b:c=2:4:5,可设a=2k,b=4k,c=5k≠0.再利用正弦定理代入即可得出.
解答:
解:∵a:b:c=2:4:5,
设a=2k,b=4k,c=5k≠0.
由正弦定理可得:
=
=
=
.
设a=2k,b=4k,c=5k≠0.
由正弦定理可得:
| 2sinB |
| 3sinC-5sinA |
| 2b |
| 3c-5a |
| 2×4k |
| 3×5k-5×2k |
| 8 |
| 5 |
点评:本题考查了正弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若函数f(x)在x=a处有导数,则
为( )
| lim |
| h→a |
| f(h)-f(a) |
| h-a |
| A、f(a) | B、f′(a) |
| C、f′(h) | D、f(h) |
 如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是( )
如图,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知cos2α-cos2β=a,那么sin(α+β)sin(α-β)等于( )
A、-
| ||
B、
| ||
| C、-a | ||
| D、a |
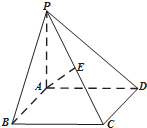 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,AB=2,AD=2