题目内容
已知二次函数 ,
, ,
,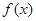 的最小值为
的最小值为 .
.
⑴求函数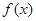 的解析式;
的解析式;
⑵设 ,若
,若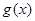 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
⑶设函数 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[
(1) ;(2)
;(2)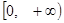 ;(3)
;(3)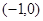 。
。
解析试题分析:(1)由 可设
可设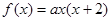 ,再由
,再由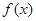 的最小值
的最小值 求a的值;(2)首先对
求a的值;(2)首先对
二次项系数分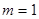 、
、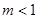 、
、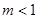 三种情况讨论,然后确定对称轴
三种情况讨论,然后确定对称轴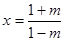 与给定区间
与给定区间 端点的关系;(3)要满足题意,须有
端点的关系;(3)要满足题意,须有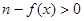 有解,且
有解,且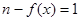 无解.然后求
无解.然后求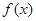 的最小值,令
的最小值,令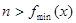 ,但
,但 不属于
不属于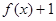 的值域,即可得实数
的值域,即可得实数 的取值范围。
的取值范围。
⑴ 由题意设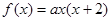 ,
,
∵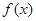 的最小值为
的最小值为 , ∴
, ∴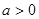 ,且
,且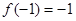 , ∴
, ∴ 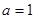 ,
,
∴ .
.
⑵ ∵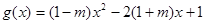 ,
,
①当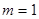 时,
时,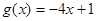 在[-1, 1]上是减函数,∴
在[-1, 1]上是减函数,∴ 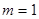 符合题意.
符合题意.
② 当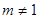 时,对称轴方程为:
时,对称轴方程为: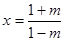 ,
,
ⅰ)当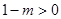 ,即
,即 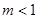 时,抛物线开口向上,
时,抛物线开口向上,
由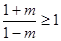 , 得
, 得 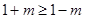 , ∴
, ∴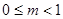 ;
;
ⅱ)当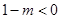 , 即
, 即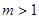 时,抛物线开口向下,
时,抛物线开口向下,
由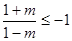 ,得
,得 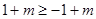 , ∴
, ∴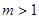 .
.
综上知,实数 的取值范围为
的取值范围为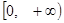 .
.
⑶法一:∵ 函数 在定义域内不存在零点,必须且只须有
在定义域内不存在零点,必须且只须有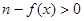 有解,且
有解,且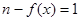 无解.
无解.
∴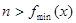 ,且
,且 不属于
不属于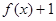 的值域,
的值域,
又∵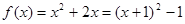 ,
,
∴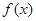 的最小值为
的最小值为 ,
,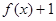 的值域为
的值域为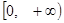 ,
,
∴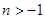 ,且
,且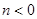
∴ 的取值范围为
的取值范围为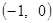 .
.
法二: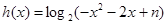 ,令
,令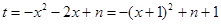 ,
,
必有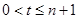 ,得
,得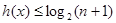 ,
,
因为函数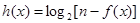 在定义域内不存在零点,
在定义域内不存在零点,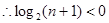 ,
,
得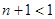 ,即
,即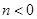 ,又
,又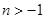 (否则函数定义域为空集,不是函数),
(否则函数定义域为空集,不是函数),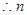 的取值范围是
的取值范围是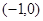 。
。
考点:(1)待定系数法求函数的解析式;(2)二次项系数及二次函数对称轴与给定区间引起的分类讨论;(3)构造函数研究函数的零点个数。

练习册系列答案
相关题目
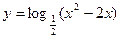 的单调递增区间是_________________.
的单调递增区间是_________________. 若存在
若存在 ,
, 成立,则称
成立,则称 为
为
 时,求函数
时,求函数 ,函数
,函数 的取值范围.
的取值范围. 其中
其中 且
且 .
.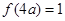 ,求
,求 的值;
的值; 上
上 恒成立,求
恒成立,求 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完. (万元)关于年产量
(万元)关于年产量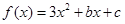 ,不等式
,不等式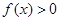 的解集为
的解集为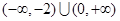 .
.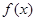 的解析式;
的解析式; 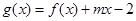 在
在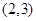 上单调,求实数
上单调,求实数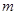 的取值范围;
的取值范围;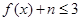 都成立,求实数n的最大值.
都成立,求实数n的最大值. 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.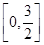 上的最大值.
上的最大值.