题目内容
某厂生产某种产品的年固定成本为250万元,每生产 万件,需另投入的成本为
万件,需另投入的成本为 (单位:万元),当年产量小于80万件时,
(单位:万元),当年产量小于80万件时, ;当年产量不小于80万件时,
;当年产量不小于80万件时, .假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
.假设每万件该产品的售价为50万元,且该厂当年生产的该产品能全部销售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数关系式;
(万件)的函数关系式;
(2)年产量为多少万件时,该厂在该产品的生产中所获利润最大?最大利润是多少?
(1) ;(2)100万件,1000万元
;(2)100万件,1000万元
解析试题分析:(1)利润 销售额
销售额 成本,销售额
成本,销售额 销售量
销售量 单价,设年产量为
单价,设年产量为 (万件),当
(万件),当  时,销售额
时,销售额 ,成本
,成本 ; 当
; 当 时,销售额
时,销售额 ,成本
,成本 ;(2)转化为求
;(2)转化为求 的最大值即可,注意解决实际问题的基本步骤:审题、建模、解模、还原。
的最大值即可,注意解决实际问题的基本步骤:审题、建模、解模、还原。
(1)当 时,
时, ;
;
当 时,
时, .
.
所以 6′
6′
(2)当
 8′
8′
当 时,
时, ,当且仅当
,当且仅当 ,即
,即 时,等号成立,所以
时,等号成立,所以 . 11′
. 11′
综上,当 时,
时, 取得最大值
取得最大值 ,即年产量为100万件时,该厂在这一产品的生产中所获利润最大,最大利润是1000万元. 12′
,即年产量为100万件时,该厂在这一产品的生产中所获利润最大,最大利润是1000万元. 12′
考点:(1)求分段函数的解析式及最值;(2)基本不等式在求最值中的应用。

练习册系列答案
相关题目
 上恒有f(x)
上恒有f(x)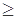 -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围. 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于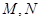 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
. 表示为
表示为 的函数;
的函数; 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.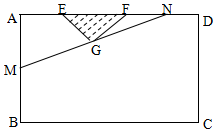
 ,
, ,
,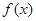 的最小值为
的最小值为 .
. ,若
,若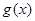 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[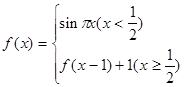 ,求
,求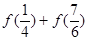 的值。
的值。 .
. 的解集;
的解集;
 ,若
,若 对任意的
对任意的 都成立,求
都成立,求 的取值范围.
的取值范围.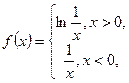 则
则 的解集为________.
的解集为________.