题目内容
已知二次函数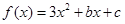 ,不等式
,不等式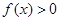 的解集为
的解集为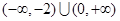 .
.
(1)求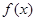 的解析式;
的解析式;
(2)若函数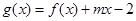 在
在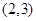 上单调,求实数
上单调,求实数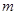 的取值范围;
的取值范围;
(3)若对于任意的x∈[-2,2],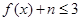 都成立,求实数n的最大值.
都成立,求实数n的最大值.
(1) 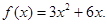 ,(2)
,(2)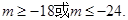 (3)-21.
(3)-21.
解析试题分析:(1) 根据一元二次方程的根与一元二次不等式的解集关系,可列出两个独立条件,求出解析式. 依题得,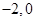 为方程
为方程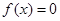 的两个实根,
的两个实根,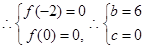
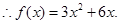
(2)二次函数单调性主要研究对称轴与定义区间相对位置关系,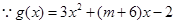 在
在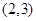 上单调,二次函数开口向上,对称轴
上单调,二次函数开口向上,对称轴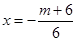
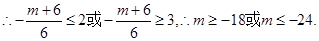 (3)恒成立问题,一般利用变量分离转化为最值问题. 依题得,
(3)恒成立问题,一般利用变量分离转化为最值问题. 依题得,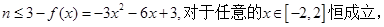 只要
只要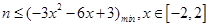 ,设
,设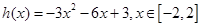
当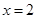 时,
时,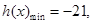
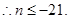 实数n的最大值为
实数n的最大值为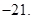
解:(1)依题得,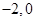 为方程
为方程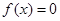 的两个实根, (2分)
的两个实根, (2分)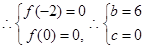 (4分)
(4分)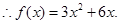 (5分)
(5分)
(2)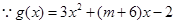 在
在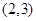 上单调,
上单调,
又二次函数开口向上,对称轴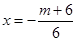 , (7分)
, (7分)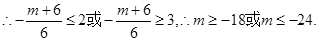 (10分)
(10分)
(3)依题得,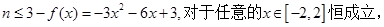 (12分)
(12分)
只要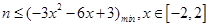 , (13分)
, (13分)
设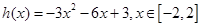
当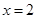 时,
时,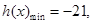 (15分)
(15分)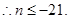 (16分)
(16分)
考点:一元二次方程的根与一元二次不等式的解集关系,二次函数单调性,不等式恒成立

练习册系列答案
相关题目
 =
=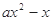 (
( ,
,
 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; 与
与 的图像有两个不同的交点
的图像有两个不同的交点 ,求
,求 的取值范围。
的取值范围。 和
和 (
( 是函数
是函数 的切线以
的切线以 为切点,求证
为切点,求证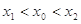 .
. 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. ,
, ,
,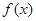 的最小值为
的最小值为 .
. ,若
,若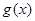 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.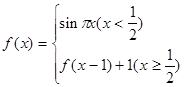 ,求
,求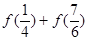 的值。
的值。 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围. 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
