题目内容
已知函数 为偶函数.
为偶函数.
(1)求 的值;
的值;
(2)若方程 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)  或
或 .
.
解析试题分析:(1)法一:根据 为偶函数,将等式
为偶函数,将等式 化简整理即可得到
化简整理即可得到 的值;法二:根据
的值;法二:根据 为偶函数,得到
为偶函数,得到 即
即 ,从中求解即可得到
,从中求解即可得到 ,检验此时是否满足
,检验此时是否满足 即可;(2)首先将方程
即可;(2)首先将方程 化简:
化简:


 ;由
;由 得
得

 ,进而可得
,进而可得 ,令
,令 ,则*变为关于
,则*变为关于 的方程
的方程 只有一个正实数根,先考虑
只有一个正实数根,先考虑 的情形是否符合,然后针对二次方程的根的分布分该方程有一正一负根、有两个相等的正根进行讨论求解,并保证
的情形是否符合,然后针对二次方程的根的分布分该方程有一正一负根、有两个相等的正根进行讨论求解,并保证 即可,最后根据各种情况讨论的结果写出
即可,最后根据各种情况讨论的结果写出 的取值范围的并集即可.
的取值范围的并集即可.
(1)法一:因为 为偶函数,所以
为偶函数,所以
即
 ,∴
,∴
∴ ,∴
,∴ 6分
6分
法二:因为 为偶函数,所以
为偶函数,所以 即
即 ,解得
,解得
此时 ,
,
 ,所以
,所以 .
.
(2)依题意知: 



∴由 得
得


 8分
8分
令 ,则①变为
,则①变为 ,只需关于
,只需关于 的方程只有一个正根即可满足题意
的方程只有一个正根即可满足题意
(1) 不合题意 9分
不合题意 9分
(2)①式有一正一负根,则 经验证满足
经验证满足 ,
, 11分
11分
(3)若①式有两相等正根,则 ,此时
,此时
若 ,则
,则 ,此时方程
,此时方程 无正根
无正根
故 舍去 13分
舍去 13分
若 ,则
,则 ,且
,且
因此
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 ,
, ,
,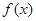 的最小值为
的最小值为 .
. ,若
,若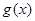 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[ 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围. 其中0
其中0
 上恒成立?
上恒成立? .
. 的解集;
的解集;
 ,若
,若 对任意的
对任意的 都成立,求
都成立,求 的取值范围.
的取值范围. 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.

 满足
满足 ,当
,当 时,
时, ,且
,且 .
. 的值;
的值; 的方程
的方程 有解,求
有解,求 的取值范围.
的取值范围. AB,tan∠FED=
AB,tan∠FED= ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.