题目内容
设函数 其中
其中 且
且 .
.
(1)已知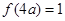 ,求
,求 的值;
的值;
(2)若在区间 上
上 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) .(2)
.(2) .
.
解析试题分析:对于(1)直接把 代入
代入 运用对数运算解得:
运用对数运算解得: ;对于(2)函数问题要注意定义域优先考虑,故对数真数恒大于零,即:
;对于(2)函数问题要注意定义域优先考虑,故对数真数恒大于零,即: ,由
,由 得:
得: ,由函数的单调性分类讨论
,由函数的单调性分类讨论 的范围,由
的范围,由 且
且 ,
, 得:
得: 和
和 .
.
(1) .
.
(2)
由 得
得 由题意知
由题意知 故
故 ,
,
从而 ,故函数
,故函数 在区间
在区间 上单调递增.
上单调递增.
①若 则
则 在区间
在区间 上单调递减,所以
上单调递减,所以 在区间
在区间 上的最大值为
上的最大值为 ,即
,即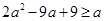 ,解得
,解得 ,又
,又 ,所以
,所以 .
.
②若 则
则 在区间
在区间 上单调递增,所以
上单调递增,所以 在区间
在区间 上的最大值为
上的最大值为 ,
, ,
,
解得 ,与
,与 联立无解.
联立无解.
综上: .
.
考点:1.对数函数的运算 2.对数函数的单调性 3.对数的最值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元. ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值; 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 是边长为
是边长为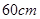 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
. 最大,试问
最大,试问 应取何值?
应取何值? 最大,试问
最大,试问

 ,
, ,
,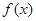 的最小值为
的最小值为 .
. ,若
,若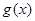 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围; ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围. 其中0
其中0
 上恒成立?
上恒成立? ,若
,若 ,则a的取值范围是 .
,则a的取值范围是 .