题目内容
5.命题:“?x∈R,sinx≤1”的否定是( )| A. | ?x∈R,sinx>1 | B. | ?x∈R,sinx≤1 | C. | ?x∈R,sinx>1 | D. | ?x∈R,sinx≥1 |
分析 根据全称命题否定的方法,结合已知中原命题,可得答案.
解答 解:命题:“?x∈R,sinx≤1”为全称命题,全称命题的否定是特称命题,
即?x∈R,sinx>1,
故选C.
点评 本题考查的知识点是命题的否定,难度不大,属于基础题.

练习册系列答案
相关题目
13.若集合A={x|y=lg(2x+3)},B={-2,-1,1,3},则A∩B等于( )
| A. | {3} | B. | {-1,3} | C. | {-1,1,3} | D. | {-1,-1,1,3} |
20.将函数y=3sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{2}$个单位长度,所得图象对应的函数( )
| A. | 在区间($\frac{π}{12}$,$\frac{7π}{12}$)上单调递减 | B. | 在区间($\frac{π}{12}$,$\frac{7π}{12}$)上单调递增 | ||
| C. | 在区间(-$\frac{π}{6}$,$\frac{π}{3}$)上单调递减 | D. | 在区间(-$\frac{π}{6}$,$\frac{π}{3}$)上单调递增 |
17.已知直线l1:2x-y+1=0,直线l2与l1关于直线y=-x对称,则直线l2的方程为( )
| A. | x-2y+1=0 | B. | x+2y+1=0 | C. | x-2y-1=0 | D. | x+2y-1=0 |
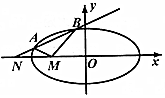 已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).
已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).