题目内容
下列命题:
①?x∈R,x2+2>0;
②?x∈N,x4≥1;
③?x∈Z,x2<1;
④?x∈Q,x2=3.
其中正确命题的个数为( )
①?x∈R,x2+2>0;
②?x∈N,x4≥1;
③?x∈Z,x2<1;
④?x∈Q,x2=3.
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:由x2为非负数,即可判断①;举反例,比如x=0,则x4=0<1,即可判断②;
举x=0,x2=0<1,即可判断③;由于x2=3,即有x=±
为无理数,即可判断④.
举x=0,x2=0<1,即可判断③;由于x2=3,即有x=±
| 3 |
解答:
解:对于①,?x∈R,x2+2≥2>0,则①对;
对于②,若x=0,则x4=0<1,则②错;
对于③,当x=0时,x2=0<1,则③对;
对于④,由于x2=3,即有x=±
为无理数,则④错.
则其中正确的有2个命题.
故选B.
对于②,若x=0,则x4=0<1,则②错;
对于③,当x=0时,x2=0<1,则③对;
对于④,由于x2=3,即有x=±
| 3 |
则其中正确的有2个命题.
故选B.
点评:本题考查全称性命题和存在性命题的真假,注意运用举反例和证明的方法,考查运算和判断能力,属于基础题和易错题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
当x∈[-3,0]时,函数y=x2+2x+3的最小值是( )
| A、1 | B、2 | C、3 | D、4 |
已知a,b为非零实数,且a<b,则下列命题成立的是( )
| A、a2<b2 | ||||
| B、a2b<a3 | ||||
C、
| ||||
D、
|
函数f(x)=1-2|x|的图象大致是( )
A、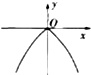 |
B、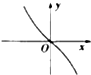 |
C、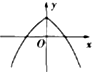 |
D、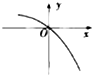 |
已知P为椭圆C上一点,F1,F2为椭圆的焦点,且|F1F2|=2
,若|PF1|与|PF2|的等差中项为|F1F2|,则椭圆C的标准方程为( )
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
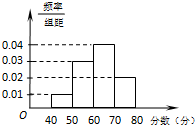 在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有
在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有