题目内容
已知实数x,y满足x-y+1=0(-1≤x≤4),则(x-3)2+y2的取值范围是 ;
的取值范围是 .
| y-2 |
| x |
考点:直线与圆的位置关系
专题:直线与圆
分析:(x-3)2+y2的表示线段MN:x-y+1=0(-1≤x≤4)上的点(x,y)到A(3,0)点的距离的平方,求得点A到直线x-y+1=0的距离以及A到点M(-1,0)的距离、A到点N(4的距离,数形结合可得(x-3)2+y2的取值范围.
由于
表示线段MN上的点(x,y)与点B(0,2)连线的斜率,求得KBM 和KBN 的值,数形结合求得
的取值范围.
由于
| y-2 |
| x |
| y-2 |
| x |
解答:
 解:如图:(x-3)2+y2的表示线段MN:x-y+1=0(-1≤x≤4)上的点(x,y)到A(3,0)点的距离的平方,
解:如图:(x-3)2+y2的表示线段MN:x-y+1=0(-1≤x≤4)上的点(x,y)到A(3,0)点的距离的平方,
点A到直线x-y+1=0的距离为
=2
,A到点M(-1,0)的距离为4,A到点N(4,5)的距离为
=
,
故(x-3)2+y2的取值范围是为[2
,
].
由于
表示线段MN上的点(x,y)与点B(0,2)连线的斜率,而KBM=
=2,KBN=
=
,
故
的取值范围是[2,+∞)∪(-∞,
].
故答案为:[2
,
];[2,+∞)∪(-∞,
].
 解:如图:(x-3)2+y2的表示线段MN:x-y+1=0(-1≤x≤4)上的点(x,y)到A(3,0)点的距离的平方,
解:如图:(x-3)2+y2的表示线段MN:x-y+1=0(-1≤x≤4)上的点(x,y)到A(3,0)点的距离的平方,点A到直线x-y+1=0的距离为
| |3-0+1| | ||
|
| 2 |
| (4-3)2+(5-0)2 |
| 26 |
故(x-3)2+y2的取值范围是为[2
| 2 |
| 26 |
由于
| y-2 |
| x |
| 2-0 |
| 0+1 |
| 5-2 |
| 4-0 |
| 3 |
| 4 |
故
| y-2 |
| x |
| 3 |
| 4 |
故答案为:[2
| 2 |
| 26 |
| 3 |
| 4 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式、斜率公式的应用,体现了数形结合、转化的数学思想,属于基础题.

练习册系列答案
相关题目
若曲线C1:x2+y2-4x=0与曲线C2:y(y-mx-x)=0有四个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
已知a,b为非零实数,且a<b,则下列命题成立的是( )
| A、a2<b2 | ||||
| B、a2b<a3 | ||||
C、
| ||||
D、
|
函数f(x)=1-2|x|的图象大致是( )
A、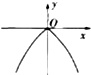 |
B、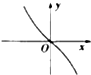 |
C、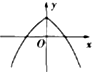 |
D、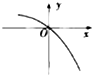 |
已知两个实数a,b(a≠b),满足aea=beb.命题p:lna+a=lnb+b;命题q:(a+1)(b+1)>0,则下列命题正确的是( )
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |