题目内容
9.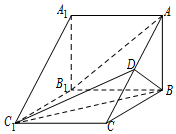 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(Ⅰ)求证:AB1∥平面BC1D;
(Ⅱ)设BC=3,求四棱锥B-DAA1C1的体积.
分析 (1)欲证AB1∥平面BC1D,只需证明AB1平行平面BC1D中的一条直线,利用三角形的中位线平行与第三边,构造一个三角形AB1C,使AB1成为这个三角形中的边,而中位线OD恰好在平面BC1D上,就可得到结论.
(2)作BE⊥AC,垂足为E,推导出AA1⊥BE,BE⊥平面AA1C1C.由此能求出四棱锥B-AA1C1D的体积.
解答 证明:连接B1C,设B1C与BC1相交于点O,连接OD,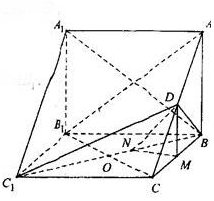
∵四边形BCC1B是平行四边形,
∴点O为B1C的中点,
∵D为AC的中点,
∴OD为△AB1C的中位线,
∴OD∥AB1,
∵OD?平面BC1D,AB1?平面BC1D,
∴AB1∥平面BC1D
(2)作BE⊥AC,垂足为E,
∵侧棱AA1⊥底面ABC,BE?底面ABC
∴AA1⊥BE
∵AA1∩AC=A
∴BE⊥平面AA1C1C.
在Rt△ABC中,BE=$\frac{AB•BC}{AC}$=$\frac{6}{\sqrt{13}}$,
∴四棱锥B-AA1C1D的体积V=$\frac{1}{3}×\frac{1}{2}$×(A1C1+AD)•AA1•BE=3.
点评 本题以三棱柱为载体,考查线面平行,考查线面角,考查面面角,解题的关键是正确运用线面平行的判定,作出线面角,面面角,计算较繁,需要细心.

练习册系列答案
相关题目
19.等比数列{an}中,公比q=2,a1+a4+a7…+a97=11,则数列{an}的前99项的和S99=( )
| A. | 99 | B. | 88 | C. | 77 | D. | 66 |
4.下列函数中,在定义域内既是奇函数又是增函数的为( )
| A. | y=3x | B. | y=2x(-1≤x<1) | ||
| C. | $y=\left\{\begin{array}{l}{x^2}+x,x>0\\{x^2}-x,x<0\end{array}\right.$ | D. | y=2x-2-x |
19.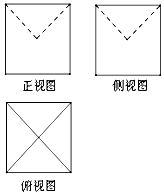 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
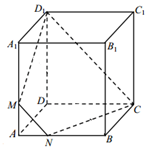 如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1
如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1