题目内容
1.已知函数f(x)=x2+2ax+2,x∈[-5,5](1)当a=-1时,求函数的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数
(3)已知函数y=x+$\frac{t}{x}$有如下性质:
如果常数t>0,那么该函数(0,$\sqrt{t}$]上是减函数,在[$\sqrt{t}$,+∞)上是增函数.
利用上述性质,直接写出函数g(x)=$\frac{f(x)}{x}$,x∈(0,5]的单调区间,并求值域.
分析 (1)直接将a=-1代入函数解析式,求出最大最小值.
(2)先求f(x)的对称轴x=-a,所以若y=f(x)在区间[-5,5]上是单调函数,则区间[-5,5]在对称轴的一边,所以得到-a≤-5,或-a≥5,这样即得到了a的取值范围;
(3)利用函数y=x+$\frac{t}{x}$在(0,$\sqrt{t}$]上是减函数,在[$\sqrt{t}$,+∞)上是增函数,即可得出结论.
解答 解:(1)当a=-1时,函数f(x)=x2-2x+2=(x-1)2+1的对称轴为x=1,
∴y=f(x)在区间[-5,1]单调递减,在(1,5]单调递增,…2
且f(-5)=37,f(5)=17<37…3
∴f(x)min=f(1)=1,f(x)max=f(-5)=37…5
(2)∵f(x)=x2+2ax+2在区间[-5,5]上是单调函数,
∴对称轴x=-a∉[-5,5]…6
即-a≤-5或-a≥5,即a≥5,或a≤-5…8
(3)∵g(x)=$\frac{f(x)}{x}$=x+2a+$\frac{2}{x}$,x∈[-5,5]
且函数y=x+$\frac{t}{x}$在(0,$\sqrt{t}$]上是减函数,在[$\sqrt{t}$,+∞)上是增函数.
∴g(x)在(0,$\sqrt{2}$)单调递减,[$\sqrt{2}$,5]单调递增…10
且g($\sqrt{2}$)=2$\sqrt{2}$+2a,x→+∞时,g(x)→+∞,
∴g(x)的值域为[2$\sqrt{2}$+2a,+∞)…12
点评 本题考查了二次函数的单调性以及最大最小值问题,属于常见题型,应该熟练掌握.

练习册系列答案
相关题目
11.设f(x)是定义在R上的增函数,且对于任意的x都有f(-x)+f(x)=0恒成立,如果实数a,b满足不等式组$\left\{\begin{array}{l}{f({a}^{2}-6a+23)+f({b}^{2}-8b-2)≤0}\\{f(b+1)>f(5)}\end{array}\right.$,那么a2+b2的取值范围是( )
| A. | [9,49] | B. | (17,49] | C. | [9,41] | D. | (17,41] |
6.集合{x∈N|x≤3}还可以表示为( )
| A. | {0,1,2,3} | B. | {2,1,3} | C. | {1,2,3,4} | D. | {x|0≤x≤3} |
11.过(2,2)点与双曲线x2$-\frac{y^2}{4}=1$有共同渐近线的双曲线方程为( )
| A. | x2$-\frac{y^2}{4}=-1$ | B. | $\frac{x^2}{4}-{y^2}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{12}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{3}=1$ |
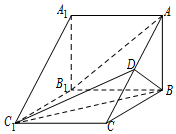 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.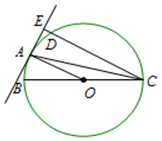 如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E
如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E