题目内容
17.若xlog23=1,则3x+9-x的值为$\frac{9}{4}$.分析 先求出x=log32,从而3x+9-x=${3}^{lo{g}_{3}2}$+$\frac{1}{{9}^{lo{g}_{3}2}}$,由此能求出结果.
解答 解:∵xlog23=1,∴x=log32,
∴3x+9-x=${3}^{lo{g}_{3}2}$+$\frac{1}{{9}^{lo{g}_{3}2}}$=2+$\frac{1}{4}$=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查指数式求解,是基础题,解题时要认真审题,注意指数、对数性质、运算法则的合理运用.

练习册系列答案
相关题目
5.已知点P(x,y)满足x2+y2<2,则满足到直线x-y+2$\sqrt{2}$=0的距离d∈[1,3]的点P概率为( )
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $\frac{1}{2}-\frac{π}{2}$ | C. | $\frac{1}{4}-\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
6.集合{x∈N|x≤3}还可以表示为( )
| A. | {0,1,2,3} | B. | {2,1,3} | C. | {1,2,3,4} | D. | {x|0≤x≤3} |
7.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=4x-1,则f(log4$\frac{1}{32}$)( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
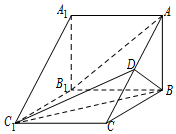 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.