题目内容

19．等比数列{an}中，公比q=2，a1+a4+a7…+a97=11，则数列{an}的前99项的和S99=（　　）
A．99B．88C．77D．66

分析 根据等比数列前n项和公式建立方程关系进行求解即可．

解答 解：∵等比数列{an}中，公比q=2，a1+a4+a7…+a97=11，
∴$\frac{{a}_{1}[1-（{q}^{3}）^{33}]}{1-{q}^{3}}$=11，①
而S99=$\frac{{a}_{1}（1-{q}^{99}）}{1-q}$②，
两式相比得$\frac{{S}_{99}}{11}$=$\frac{1-{q}^{3}}{1-q}$=$\frac{1-8}{1-2}$=7，
即S99=77，
故选：C

点评 本题主要考查数列求解的计算，根据等比数列前n项和公式建立方程思想是解决本题的关键．

练习册系列答案
相关题目
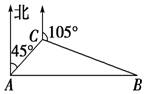9．一商船行至索马里海域时，遭到海盗的追击，随即发出求救信号．正在该海域执行护航任务的海军“黄山”舰在A处获悉后，即测出该商船在方位角为45°距离10海里的C处，并沿方位角为105°的方向，以9海里/时的速度航行．“黄山”舰立即以21海里/时的速度前去营救．如图所示，求“黄山”舰靠近商船所需要的最少时间及所经过的路程．
10．△ABC中，角A，B，C的对边分别是a，b，c，已知b=c，sinA=1-$\frac{a^2}{{2{b^2}}}$，则A=$\frac{π}{4}$．
7．过抛物线y2-2x=0的焦点且倾斜角为45°的直线交抛物线于A，B两点，求$\overrightarrow{OA}$•$\overrightarrow{OB}$．
14．已知圆的方程为x2+y2=1，则圆心到直线x+y+2=0的距离为（　　）
A．1B．2C．2$\sqrt{2}$D．$\sqrt{2}$
4．中心在原点，一焦点为${F_1}（0，-5\sqrt{2}）$的椭圆截直线y=3x-2所得弦的中点的横坐标为$\frac{1}{2}$，求此椭圆的方程．
11．设f（x）是定义在R上的增函数，且对于任意的x都有f（-x）+f（x）=0恒成立，如果实数a，b满足不等式组$\left\{\begin{array}{l}{f（{a}^{2}-6a+23）+f（{b}^{2}-8b-2）≤0}\\{f（b+1）＞f（5）}\end{array}\right.$，那么a2+b2的取值范围是（　　）
A．[9，49]B．（17，49]C．[9，41]D．（17，41]
8．等比数列{an}的前n项和为Sn，若a1=1，$\frac{{{S_{10}}}}{S_5}=\frac{33}{32}$．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设bn=$\frac{3n-1}{a_n}$，求数列{bn}的前n项和Tn．
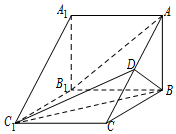9．（文科）如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．
（Ⅰ）求证：AB1∥平面BC1D；
（Ⅱ）设BC=3，求四棱锥B-DAA1C1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网