题目内容
14.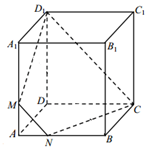 如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1
如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1(1)求证:平面AMN∥平面DD1C
(2)平面 MNCD1将此正方体分为两部分,求这两部分的体积之比.
分析 (1)推导出AN∥平面DD1C,AM∥平面DD1C,由此能证明平面AMN∥平面DD1C.
(2)记平面MNCD1 将正方体分成两部分的下部分体积为V1,上部分体积为V2,连接D1A,D1N,DN,则几何体 D1-AMN,D1-ADN,D1-CDN均为三棱锥,由此能求出平面 MNCD1分此正方体的两部分体积的比.
解答 证明:(1)在正方体ABCD-A1B1C1D1中,
∵M,N 分别是棱 AA1,AB上的点,且 AM=AN=1,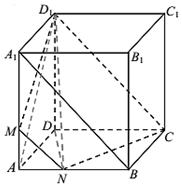
∴AN∥DC,
又∵DC?平面DD1C,AN?平面DD1C,
∴AN∥平面DD1C,
同理,AM∥平面DD1C,
又∵AM∩AN=A,∴平面AMN∥平面DD1C.
解:(2)记平面MNCD1 将正方体分成两部分的下部分体积为V1,上部分体积为V2,
如图,连接D1A,D1N,DN,则几何体 D1-AMN,D1-ADN,D1-CDN均为三棱锥,
∴${V}_{1}={V}_{{D}_{1}-AMN}+{V}_{{D}_{1}-ADN}+{V}_{{D}_{1}-CDN}$
=$\frac{1}{3}{S}_{△AMN}•{D}_{1}{A}_{1}$+$\frac{1}{3}{S}_{△ADN}•{D}_{1}D$+$\frac{1}{3}{S}_{△CDN}•{D}_{1}D$
=$\frac{1}{3}×\frac{1}{2}×3+\frac{1}{3}×\frac{3}{2}×3+\frac{1}{3}×\frac{9}{2}×3$
=$\frac{13}{2}$,
从而${V}_{2}={V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}-{V}_{AMN-{D}_{1}C}$=27-$\frac{13}{2}$=$\frac{41}{2}$,
∴$\frac{{V}_{1}}{{V}_{2}}=\frac{13}{41}$.
所以平面MNCD1分此正方体的两部分体积的比为$\frac{13}{41}$.
点评 本题考查面面平行的证明,考查平面分正方体的两部分体积的比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $\frac{1}{2}-\frac{π}{2}$ | C. | $\frac{1}{4}-\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
| A. | {0,1,2,3} | B. | {2,1,3} | C. | {1,2,3,4} | D. | {x|0≤x≤3} |
| A. | M=P | B. | P?M | C. | M?P | D. | M∪P=R |
| A. | 椭圆或圆 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
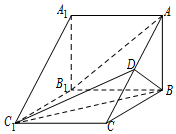 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.