题目内容
4.下列函数中,在定义域内既是奇函数又是增函数的为( )| A. | y=3x | B. | y=2x(-1≤x<1) | ||
| C. | $y=\left\{\begin{array}{l}{x^2}+x,x>0\\{x^2}-x,x<0\end{array}\right.$ | D. | y=2x-2-x |
分析 根据一次函数的单调性,二次函数在定义域上的单调性,指数函数的奇偶性即可判断A,B,C错误,根据奇函数的定义及函数导数符号和函数单调性的关系即可判断出D正确.
解答 解:A、根据指数函数y=3x的图象知其在定义域上没有奇偶性;
B、一次函数y=2x(-1≤x<1)定义域不对称,不是奇函数;
C、函数其定义域上没有单调性;
D、y=2x-2-x是奇函数,且y′=ln2(2x+2-x)>0,∴该函数在定义域R上是增函数.
故选D.
点评 考查一次函数、二次函数在定义域上的单调性,指数函数的奇偶性,以及奇函数的定义,函数导数符号和函数单调性的关系.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
14.已知圆的方程为x2+y2=1,则圆心到直线x+y+2=0的距离为( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
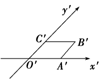 在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.
在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.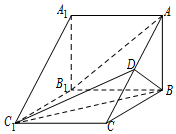 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.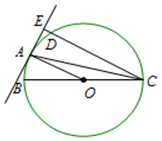 如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E
如图所示,BC 为⊙O 的直径,$\widehat{AB}=\widehat{AD}$,以点 A 为切点的切线与 CD 的延长线交于点E