题目内容
已知数列{an}满足an+1=2（n+1）•5n•an，a1=3，求数列{an}的通项公式．
考点：数列递推式
专题：等差数列与等比数列
分析：由题意得
=2（n+1）•5n，利用累乘法求数列的通项公式．
| an+1 |
| an |
解答：
解：∵an+1=2（n+1）•5n•an，a1=3，
∴
=2（n+1）•5n，
∴n≥2时，an=a1•
•
…
=3×（2×2×51）（2×3×52）…（2n•5n-1）
=3×2n-1×51+2+3+…+（n-1）•（2×3×4×…×n）
=3n!×2n-1×5
．
∴
| an+1 |
| an |
∴n≥2时，an=a1•
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
=3×2n-1×51+2+3+…+（n-1）•（2×3×4×…×n）
=3n!×2n-1×5
| n(n-1) |
| 2 |
点评：本题主要考查求数列通项公式的方法累乘法的运用能力及学生的运算求解能力，属基础题．
练习册系列答案
相关题目
f（x）为奇函数，且在（-∞，0）上为增函数，g（x）为偶函数 且在（-∞，0）上为增函数 则在（0，+∞）上（ ）
| A、两个都是增函数 |
| B、两个都是减函数 |
| C、f（x）为增函数g（x）为减函数 |
| D、f（x）为减函数g（x）为增函数 |
已知函数f（x）=cos2x-tcosx在x∈[
，
]上为单调递增函数，则实数t的取值范围是（ ）
| π |
| 6 |
| π |
| 3 |
A、[2
| ||
B、[
| ||
| C、（-∞，2] | ||
| D、（-∞，1] |
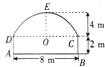如图所示的图形为一隧道的截面，其中ABCD是矩形，CED是抛物线的一段，在工程的设计中，要注意开凿隧道所需挖掘的土石方量，这就需要计算这个截面的面积，试根据图中所给出的数据计算这个截面的面积．