题目内容
16.用0,1,2,3,4,组成没有重复数字的四位数,个位数与十位数的差的绝对值不超过2,这样的四位数的个数是64.分析 根据题意,按照个位数字的不同分5种情况讨论:即①、个位数字为0,②、个位数字为1,③、个位数字为2,④、个位数字为3,⑤、个位数字为4,每种情况下先分析十位数字的情况,再分析千位、百位数字的情况,由分步计数原理可得每种情况下的四位数数字的数目,由分类计数原理计算可得答案.
解答 解:根据题意,按照个位数字的不同分5种情况讨论:
①、个位数字为0时,
十位数字可以是1或2,有2种情况,在剩余的3个数字中任取2个,放在千位、百位,有A32=6种情况,
此时有2×6=12个符合条件的四位数;
②、个位数字为1时,
十位数字可以是0或2或3,有3种情况,
若十位数字为0,可以在剩余的3个数字中任取2个,放在千位、百位,有A32=6种情况,
若十位数字为2或3,千位数字不能为0,有2种情况,百位数字也有2种情况,有2×2×2=8种情况,
此时有6+2×2×2=14个符合条件的四位数;
③、个位数字为2时,
十位数字可以是0或1或3或4,有4种情况,
若十位数字为0,可以在剩余的3个数字中任取2个,放在千位、百位,有A32=6种情况,
若十位数字为1或3或4,千位数字不能为0,有2种情况,百位数字也有2种情况,有3×2×2=12种情况,
此时有6+3×2×2=18个符合条件的四位数;
④、个位数字为3时,
十位数字可以是1或2或4,有3种情况,
千位数字不能为0,有2种情况,百位数字也有2种情况,
此时有3×2×2=12个符合条件的四位数;
⑤、个位数字为4时,
十位数字可以是2或3,有2种情况,
千位数字不能为0,有2种情况,百位数字也有2种情况,
此时有2×2×2=8个符合条件的四位数;
则一共有12+14+18+12+8=64个符合条件的四位数;
故答案为:64.
点评 本题考查排列组合的运用,涉及分类计数原理,关键是结合题意进行分类讨论,需要注意千位数字不能为0.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | 9 | B. | 15 | C. | 18 | D. | 36 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
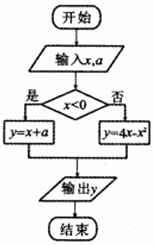
| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |
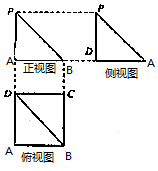 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.