题目内容
4.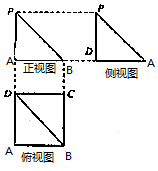 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形,俯视图为一个矩形与它的一条对角线.(1)用斜二测画法画出这个几何体的直观图;
(2)求该几何体的表面积;
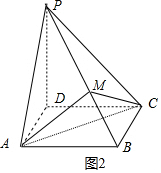
(3)在几何体直图中,在线段PB上是否得在点M,使得PB⊥平面MAC,若得在,求线段PM的长,若不存在,请说明理由.
分析 (1)三视图复原几何体是四棱锥,一条侧棱垂直底面正方形,考查正方体的图形,即可得到这样的几何体.
(2)利用体积公式求解;
(3)AC⊥面PDB⇒PB⊥AC,要使PB⊥平面MAC,只需PB⊥AM即可,过A作AM⊥PB与M即可,利用面积等求AM.再求PM
解答 解:(1)视图复原的几何体是底面为 正方形,侧棱垂直底面,是正方体的一部分,几何体的直观图如图1所示;
(2)sADP=SCDP=$\frac{1}{2}×4×4=8$,
∵AB⊥面PAD,BC⊥面PDC,∴SPBC=SPBA=$\frac{1}{2}×4×4\sqrt{2}=8\sqrt{2}$
∴该几何体的表面积s=8×2+8$\sqrt{2}$×2+16=32+16$\sqrt{2}$.
(3)∵AC⊥DB,AC⊥PD,PD∩DB=D,∴AC⊥面PDB⇒PB⊥AC,
要使PB⊥平面MAC,只需PB⊥AM即可,
∴过A作AM⊥PB与M即可,
在Rt△PAB中,PA•AB=PB•AM⇒4$\sqrt{2}$×4=4$\sqrt{3}$×AM⇒AM=$\frac{4\sqrt{6}}{3}$,
∴$PM=\sqrt{P{A}^{2}-A{M}^{2}}=\frac{8\sqrt{3}}{3}$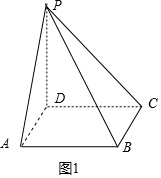
点评 本题考查了三视图,及几何体的表面积、线面垂直的动点问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 60-12π | B. | 60-6π | C. | 72-12π | D. | 72-6π |
 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.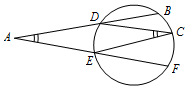 所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.
所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.