题目内容
已知命题P:方程x2+mx+1=0有实根,Q:不等式x2-2x+m>0的解集为R,若命题P或Q是假命题,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:由命题P或Q是假命题,可得命题P与Q同时为假,
则方程x2+mx+1=0无实根,且不等式x2-2x+m>0的解集不为R同时成立,
再结合二次函数的根与其判别式的关系解题.
则方程x2+mx+1=0无实根,且不等式x2-2x+m>0的解集不为R同时成立,
再结合二次函数的根与其判别式的关系解题.
解答:
解:若命题P或Q是假命题,则命题P与Q同时为假,
∴方程x2+mx+1=0无实根,且不等式x2-2x+m>0的解集不为R同时成立,
一方面,方程x2+mx+1=0无实根,则△=m2-4<0,∴-2<m<2;
另一方面,不等式x2-2x+m>0的解集不为R,则△=4-4m≥0,∴m≤1,
综上两方面,-2<m≤1,
实数m的取值范围为{m|-2<m≤1}
∴方程x2+mx+1=0无实根,且不等式x2-2x+m>0的解集不为R同时成立,
一方面,方程x2+mx+1=0无实根,则△=m2-4<0,∴-2<m<2;
另一方面,不等式x2-2x+m>0的解集不为R,则△=4-4m≥0,∴m≤1,
综上两方面,-2<m≤1,
实数m的取值范围为{m|-2<m≤1}
点评:本题主要考查了复合函数真假的判断,真值表的运用,二次函数图象和性质,一元二次不等式的解法,转化化归的思想方法,属基础题

练习册系列答案
相关题目
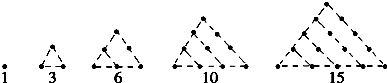
把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图所示).则第七个三角形数是( )

| A、27 | B、28 | C、29 | D、30 |