将数30012(4)转化为十进制数为( )A．524B．260C．256D．774 题目和参考答案——青夏教育精英家教网——

题目内容

13．将数30012_（4）转化为十进制数为（　　）

A．

524

B．

260

C．

256

D．

774

分析用所给的四进制的数字从最后一个数字开始乘以4的0次方，1次方，2次方，3次方，4次方，最后累加求和得到结果．

解答解：30012_（4）=2+1×4+3×4⁴=2+4+32+768=774．
故选：D．

点评本题考查进位制，本题解题的关键是理解进位制之间的转化原则，注意数字的运算不要出错，本题是一个基础题．

练习册系列答案

名师优选卷系列答案

青海省中考模拟试卷系列答案

中考指导系列答案

习题e百课时训练系列答案

68所名校图书小学毕业升学考前突破系列答案

一通百通系统归类总复习系列答案

新动力系列答案

一路领先大提速同步训练与测评系列答案

中考导航总复习系列答案

中考快递同步检测系列答案

相关题目

3．如图所示，正方体ABCD-A′B′C′D′的棱长为1，O是平面A′B′C′D′的中心，则O到平面ABC′D′的距离是（　　）

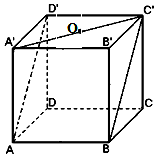
$\frac{\sqrt{2}}{4}$

$\frac{\sqrt{2}}{2}$

$\frac{\sqrt{3}}{2}$

4．已知随机变量X服从二项分布B（n，p），若E（X）=30，D（X）=20，则n，p分别等于（　　）

n=45，p=$\frac{2}{3}$

n=45，p=$\frac{1}{3}$

n=90，p=$\frac{1}{3}$

n=90，p=$\frac{2}{3}$

1．下列5个判断：
①若f（x）=x²-2ax在[1，+∞）上增函数，则a=1；
②函数y=2^x为R上的单调递增的函数；
③函数y=ln（x²+1）的值域是R；
④函数y=2^|x|的最小值是1；
⑤在同一坐标系中函数y=2^x与y=2^-x的图象关于y轴对称．
其中正确的是②④⑤．

8．已知sinx+cosx=$\frac{1}{5}$（0≤x＜π），则tanx的值等于（　　）

18．已知函数f（x）=xlnx，g（x）=ax²-（a+1）x+1（a∈R）．
（Ⅰ）当a=0时，设h（x）=f（x）+g（x），求h（x）的单调区间；
（Ⅱ）当x≥1时，f（x）≤g（x）+lnx，求实数a的取值范围．

5．设点M（x₀，1），设在圆O：x²+y²=1上存在点N，使得∠OMN=30°，则实数x₀的取值范围为$[-\sqrt{3}，\sqrt{3}]$．

2．已知函数f（x）=x²-ax的图象在点A（1，f（1））处的切线l与直线x+3y+2=0垂直，若数列{$\frac{1}{f（n）}$}的前n项和为S_n，则S₂₀₁₇的值为$\frac{2017}{2018}$．

3．已知函数f（x）=x³-12x，若f（x）在区间（2m，m+1）上单调递减，则实数m的取值范围是（　　）