题目内容
如图,在圆内画1条线段,将圆分割成两部分;画2条相交线段,将圆分割成4部分;画3条线段,将圆最多分割成7部分;画4条线段,将圆最多分割成11部分.
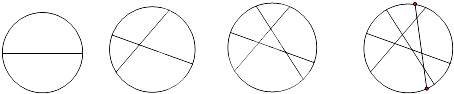
(1)记在圆内画n条线段,将圆最多分割成an部分,归纳出an+1与an的关系;
(2)猜想数列{an}的通项公式,根据an+1与an的关系及数列的知识,证明你的猜想是否成立.

(1)记在圆内画n条线段,将圆最多分割成an部分,归纳出an+1与an的关系;
(2)猜想数列{an}的通项公式,根据an+1与an的关系及数列的知识,证明你的猜想是否成立.
考点:数学归纳法,进行简单的合情推理
专题:推理和证明
分析:(1)由题意可得 a1=2,a2=4,a3=7,a4=11,再由a2-a1=2,a3-a2=3,a4-a3=4,归纳可得结论(2)猜想数列{an}的通项公式为an=
,n∈N,再用数学归纳法进行证明.
| n2+n+2 |
| 2 |
解答:
解:(1)由题意可得 a1=2,a2=4,a3=7,a4=11,
显然 a2-a1=2,a3-a2=3,a4-a3=4,归纳可得 an+1 -an=n+1.
(2)猜想数列{an}的通项公式为an=
,n∈N.
证明:①当n=1时,an=
成立,
②假设 ak=
,再根据ak+1 -ak=k+1,
可得ak+1=ak+k+1=
+k+1=
=
,
故当n=k+1时,an=
,n∈N 仍然成立.
结合①②可得,数列{an}的通项公式为an=
,n∈N.
显然 a2-a1=2,a3-a2=3,a4-a3=4,归纳可得 an+1 -an=n+1.
(2)猜想数列{an}的通项公式为an=
| n2+n+2 |
| 2 |
证明:①当n=1时,an=
| n2+n+2 |
| 2 |
②假设 ak=
| k2+k+2 |
| 2 |
可得ak+1=ak+k+1=
| k2+k+2 |
| 2 |
| k2+3k+4 |
| 2 |
| (k+1)2+(k+1)+2 |
| 2 |
故当n=k+1时,an=
| n2+n+2 |
| 2 |
结合①②可得,数列{an}的通项公式为an=
| n2+n+2 |
| 2 |
点评:本题主要考查不完全归纳法的应用,用数学归纳法证明等式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,该球的表面积是
如图所示,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,该球的表面积是