题目内容
已知x,y,z∈R+,且x+y+z=1
(1) 若2x2+3y2+6z2=1,求x,y,z的值.
(2) 若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
解:(1) ∵ (2x2+3y2+6z2)( +
+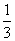 +
+ )≥(x+y+z)2=1,当且仅当
)≥(x+y+z)2=1,当且仅当 时取“=”.∴ 2x=3y=6z,
时取“=”.∴ 2x=3y=6z,
又∵ x+y+z=1,∴ x= ,y=
,y=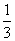 ,z=
,z= .
.
(2) ∵ (2x2+3y2+tz2)  ≥(x+y+z)2=1,∴ (2x2+3y2+tz2)min=
≥(x+y+z)2=1,∴ (2x2+3y2+tz2)min= .
.
∵ 2x2+3y2+tz2≥1恒成立,
∴ ≥1.∴ t≥6.
≥1.∴ t≥6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 .过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________.
.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么C的方程为________. -
- ≥a+
≥a+ -2.
-2.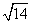 ,求x+y+z的值.
,求x+y+z的值. 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围. 对应的变换作用下变为直线l′:x+by=1.
对应的变换作用下变为直线l′:x+by=1.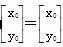 ,求点P的坐标.
,求点P的坐标. (θ为参数)交于点A、B,求PA·PB的值.
(θ为参数)交于点A、B,求PA·PB的值.