题目内容
11.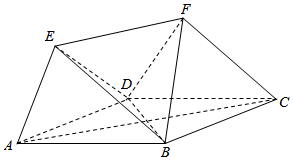 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.(1)求证:AE∥面BDF;
(2)求证:AD⊥BE.
分析 (1)设AC交BD于O点,连接OF,由余弦定理可得A0=$\sqrt{3}$=EF,又EF∥AC,即可证明AE∥FO,从而可证AE∥面BDF;
(2)取AD中点G,连接BG,EG,通过证明EG⊥AD,BG⊥AD,可证AD⊥平面EGB,即可得证AD⊥BE.
解答  证明:(1)设AC交BD于O点,连接OF,
证明:(1)设AC交BD于O点,连接OF,
∵四边形ABCD为菱形,且∠DAB=60°,AD=2,
∴∠ADC=120°,由余弦定理可得:AC2=AD2+DC2-2•AD•DC•cos∠ADC=22+22-2×2×2×cos120°=12,
∴A0=$\frac{1}{2}$AC=$\sqrt{3}$=EF,
又∵EF∥AC,
∴四边形AEFO为平行四边形,可得AE∥FO,
又∵AE?面BDF,FO?面BDF,
∴AE∥面BDF;
(2)如图,取AD中点G,连接BG,EG,
∵EA=ED,可得EG⊥AD,
∵四边形ABCD为菱形,且∠DAB=60°,可得BG⊥AD,
又∵BG∩EG=G,
∴AD⊥平面EGB,
∵BE?平面EGB,
∴AD⊥BE.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
1.已知集合A={x|-1≤x<2},B={x|1<x<4},则A∪B可表示为( )
| A. | [-1,4) | B. | (-1,4) | C. | [-1,1) | D. | (1,2) |
2.运行如图程序框图,则当输出y的值最大时,输入的x值等于( )


| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
19.已知直线y=ax+b与曲线y=ex相切,则ab的最大值是( )
| A. | $\frac{e}{2}$ | B. | e | C. | $\frac{\sqrt{e}}{2}$ | D. | $\sqrt{e}$ |
20.下列函数中,最小正周期为π的偶函数是( )
| A. | y=sin2x+cos2x | B. | $y=cos(2x+\frac{π}{2})$ | C. | y=cos(2x-1) | D. | y=cos2x |
1.过点(1,-2)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,则AB所在直线的方程为( )
| A. | y=-$\frac{\sqrt{3}}{4}$ | B. | y=-$\frac{1}{2}$ | C. | y=-$\frac{\sqrt{3}}{2}$ | D. | y=-$\frac{1}{4}$ |
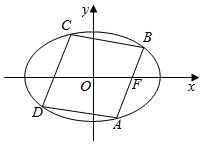 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0),菱形ABCD的各顶点在椭圆E上,且直线AB经过点F.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0),菱形ABCD的各顶点在椭圆E上,且直线AB经过点F.