题目内容
已知直线l垂直平面a,垂足为O,在矩形ABCD中AD=1,AB=2,若点A在l上移动,点B在平面a上移动,则O、D两点间的最大距离为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:先将原问题转化为平面内的最大距离问题解决,以O为原点,OA为y轴,OB为x轴建立直角坐标系,如图.设∠ABO=θ,D(x,y),D、O两点间的最大距离表示成2
sin(2θ-
)+3,最后结合三角函数的性质求出其最大值即可.
| 2 |
| π |
| 4 |
解答:
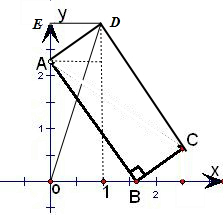 解:将原问题转化为平面内的最大距离问题解决,AD=1,AB=2,
解:将原问题转化为平面内的最大距离问题解决,AD=1,AB=2,
以O为原点,OA为y轴,OB为x轴建立直角坐标系,如图.
设∠ABO=θ,D(x,y),则有:
x=ADsinθ=sinθ,
y=ABsinθ+ADcosθ
=cosθ+2sinθ,
∴x2+y2=sin2θ+cos2θ+4sinθcosθ+4sin2θ.
=-2cos2θ+2sin2θ+3
=2
sin(2θ-
)+3,
当sin(2θ-
)=1时,x2+y2最大,为2
+3,
则D、O两点间的最大距离为1+
.
故答案为:1+
.
 解:将原问题转化为平面内的最大距离问题解决,AD=1,AB=2,
解:将原问题转化为平面内的最大距离问题解决,AD=1,AB=2,以O为原点,OA为y轴,OB为x轴建立直角坐标系,如图.
设∠ABO=θ,D(x,y),则有:
x=ADsinθ=sinθ,
y=ABsinθ+ADcosθ
=cosθ+2sinθ,
∴x2+y2=sin2θ+cos2θ+4sinθcosθ+4sin2θ.
=-2cos2θ+2sin2θ+3
=2
| 2 |
| π |
| 4 |
当sin(2θ-
| π |
| 4 |
| 2 |
则D、O两点间的最大距离为1+
| 2 |
故答案为:1+
| 2 |
点评:本题主要考查了点、线、面间的距离计算,解答关键是将空间几何问题转化为平面几何问题解决,利用三角函数的知识求最大值

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若复数z=
,则|
|等于( )
| 2i |
| 1-i |
. |
| z |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
若集合A={x|x(x-2)>0},B={x||x+1|<2},则A∩B=( )
| A、(-3,2) |
| B、(-3,0) |
| C、(0,2) |
| D、(1,2) |