题目内容
若函数f(x)=
-ax2,其中a∈R,
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有四个不同的零点,求a的取值范围.
| |x| |
| x+2 |
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有四个不同的零点,求a的取值范围.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)当a=2时,函数f(x)=
-ax2=
,令|x|-2x2(x+2)=0,可得
…①或
…②,然后解不等式组,求出函数f(x)的零点即可;
(2)当a>0,x>0时,函数f(x)=
-ax2=
=
,令f(x)=0,可得x(1-ax2-2ax)=0,解方程,求出函数f(x)在(0,+∞)内的零点即可;
(3)函数f(x)=
-ax2有四个不同的零点,①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;②当x≠0时,可得y=
与y=a(x+2)的图象在平面直角坐标系中有3个不同的交点,分别画出它们的图象,判断出a的取值范围即可.
| |x| |
| x+2 |
| |x|-2x2(x+2) |
| x+2 |
|
|
(2)当a>0,x>0时,函数f(x)=
| |x| |
| x+2 |
| x-ax3-2ax2 |
| x+2 |
| x(1-ax2-2ax) |
| x+2 |
(3)函数f(x)=
| |x| |
| x+2 |
| |x| |
| x2 |
解答:
解:(1)当a=2时,函数f(x)=
-ax2=
,
令|x|-2x2(x+2)=0,
可得
…①或
…②,
由①可得 x=0,x=
+1,或x=
-1;
由②可得x=
-1,
综上,当a=2时,函数f(x)的零点为x=0,x=
+1,x=
-1或x=
-1;
(2)当a>0,x>0时,
函数f(x)=
-ax2=
=
,
令f(x)=0,
可得x(1-ax2-2ax)=0,
解得x=-1+
,x=0(舍去),或x=-1-
(舍去),
即函数f(x)在(0,+∞)内有且仅有一个零点x=-1+
;
(3)函数f(x)=
-ax2有四个不同的零点,
①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;
②当x≠0时,可得y=
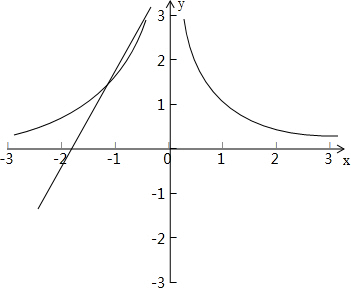
与y=a(x+2)的图象在平面直角坐标系中有3个不同的交点,
分别画出它们的图象如下:
当y=a(x+2)与y=-
相切时,a=1,
所以若函数f(x)有四个不同的零点,求a的取值范围为(1,+∞).
| |x| |
| x+2 |
| |x|-2x2(x+2) |
| x+2 |
令|x|-2x2(x+2)=0,
可得
|
|
由①可得 x=0,x=
| ||
| 2 |
| ||
| 2 |
由②可得x=
| ||
| 2 |
综上,当a=2时,函数f(x)的零点为x=0,x=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)当a>0,x>0时,
函数f(x)=
| |x| |
| x+2 |
| x-ax3-2ax2 |
| x+2 |
| x(1-ax2-2ax) |
| x+2 |
令f(x)=0,
可得x(1-ax2-2ax)=0,
解得x=-1+
| 2 |
| 2 |
即函数f(x)在(0,+∞)内有且仅有一个零点x=-1+
| 2 |
(3)函数f(x)=
| |x| |
| x+2 |
①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;
②当x≠0时,可得y=
| |x| |
| x2 |
分别画出它们的图象如下:
当y=a(x+2)与y=-
| 1 |
| x |
所以若函数f(x)有四个不同的零点,求a的取值范围为(1,+∞).

点评:本题主要考查了函数的零点与方程的根的关系,考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
所示结构图中要素之间表示从属关系是( )
A、 |
B、 |
C、 |
D、 |
 设双曲线S:
设双曲线S: