题目内容
2.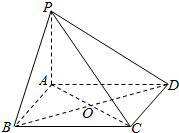 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.(1)判断CD与平面PAD是否垂直?
(2)判断平面PCD与平面PAD是否垂直?
分析 (1)由已知得PA⊥CD,AD⊥CD,由此能证明CD⊥平面PAD.
(2)由CD⊥平面PAD,CD?平面PCD,得到平面PCD⊥平面PAD.
解答 解:(1)CD⊥平面PAD.
证明如下:
∵PA垂直于正方形ABCD所在的平面,A为垂足,CD?平面ABCD,
∴PA⊥CD,∵ABCD是正方形,∴AD⊥CD,
∵PA∩AD=A,∴CD⊥平面PAD.
(2)平面PCD⊥平面PAD.
证明如下:∵CD⊥平面PAD,CD?平面PCD,
∴平面PCD⊥平面PAD.
点评 本题考查线面垂直的判断,考查面面垂直的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12. 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
(I)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表参考公式:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):(I)小明向班级同学发出倡议,为该小区居民捐款.现从损失超过6000元的居民中随机抽出2户进行捐款援助,求这两户在同一分组的概率;
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.若函数y=f(x)的图象与y=2-x的图象关于y轴对称,则f(3)=( )
| A. | 8 | B. | 4 | C. | $\frac{1}{8}$ | D. | $\frac{1}{4}$ |
17.二次曲线$\left\{\begin{array}{l}{x=4cosθ}\\{y=3sinθ}\end{array}\right.$(θ为参数)的焦点坐标为( )
| A. | (±5,0) | B. | (0,5) | C. | (±$\sqrt{7}$,0) | D. | (0,±$\sqrt{7}$) |