题目内容
13.若f(x)是定义在R上的函数,对任意的实数x都有:f(x+6)≤f(x+2)+4和f(x+4)≥f(x+2)+2,且f(1)=1,则f(2013)=2013.分析 由已知式子可得f(x+6)=f(x+2)+4,再由f(1)=1找规律可得.
解答 解:∵f(x+4)≥f(x+2)+2,
∴f(x+6)=f[(x+2)+4]≥f(x+4)+2
≥f(x+2)+2+2=f(x+2)+4,
又∵f(x+6)≤f(x+2)+4,
∴f(x+6)=f(x+2)+4,
∴f(5)=f(1)+4=5,
f(9)=f(5)+4=9,
$…\\;\\;\\;\\;\\;\\;…$ $…\\;\\;\\;\\;\\;\\;…$
f(2013)=2013
故答案为:2013
点评 本题考查函数的值,得出其中的规律是解决问题的关键,属基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.已知a>0,b>0满足a+b=2,则$\frac{1}{a}+\frac{9}{b}$的最小值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 24 |
8.椭圆$\frac{{x}^{2}}{4}$+y2=1的两个焦点为F1,F2,过F2作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF1|等于( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 4 |
18.设f(x)为奇函数,g(x)为偶函数,则下列函数中是奇函数的是( )
| A. | f(g(x)) | B. | g(f(x)) | C. | f(f(x)) | D. | g(g(x)) |
3.已知$\overrightarrow{a}$=(3,-1),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
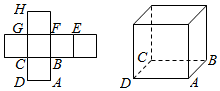 一个正方体的平面展开图及正方体的直观图的示意图如图所示:
一个正方体的平面展开图及正方体的直观图的示意图如图所示: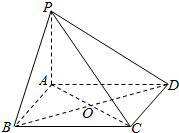 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.