题目内容
14.已知全集∪=A∪B∪C,又知card(∪)=24,card(A)=12,card(B)=10,card(C)=13,card(A∩B∩C)=2,则card((A∩B)∪(B∩C)∪(C∩A))=9.分析 作出韦恩图,根据元素个数列出方程解出.
解答 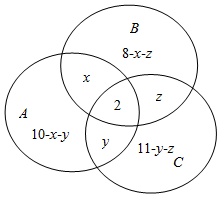 解:作出韦恩图如图所示:则全集U中的元素分为7部分,
解:作出韦恩图如图所示:则全集U中的元素分为7部分,
设card(A∩B∩∁UC)=x,card(A∩C∩∁UB)=y,card(B∩C∩∁UA)=z,
则card(∁U(B∪C))=10-x-y,card(∁U(A∪C))=8-x-z,card(∁U(A∪B))=11-y-z.
∵card(∪)=24,∴(10-x-y)+x+y+2+(8-x-z)+z+(11-y-z)=24,
∴x+y+z=7.
∴card((A∩B)∪(B∩C)∪(C∩A))=x+y+z+2=9.
故答案为:9.
点评 本题考查了元素个数的计算,使用韦恩图可使计算直观,简单.

练习册系列答案
相关题目
3.已知$\overrightarrow{a}$=(3,-1),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
9.若命题p是假命题,命题q是真命题,则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ?p是假命题 | D. | ¬q是假命题 |
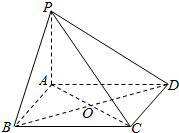 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.