题目内容
17.已知数列通项an=lg[100×$(\frac{\sqrt{2}}{2})$n-1](1)写出这个数列的前三项;
(2)求证:数列{an}是等差数列.
分析 (1)根据通项公式计算;
(2)使用对数的运算性质化简通项公式,计算an+1-an的值,判断是否为常数.
解答 解:(1)a1=lg100=2,a2=lg(100×$\frac{\sqrt{2}}{2}$)=lg100+lg$\frac{\sqrt{2}}{2}$=2+lg$\frac{\sqrt{2}}{2}$,a3=lg[100×($\frac{\sqrt{2}}{2}$)2]=lg100+lg($\frac{\sqrt{2}}{2}$)2=2+2lg$\frac{\sqrt{2}}{2}$.
(2)∵an=lg[100×$(\frac{\sqrt{2}}{2})$n-1]=lg100+lg$(\frac{\sqrt{2}}{2})$n-1=2+(n-1)lg$\frac{\sqrt{2}}{2}$.
∴an+1=2+nlg$\frac{\sqrt{2}}{2}$,∴an+1-an=nlg$\frac{\sqrt{2}}{2}$-(n-1)lg$\frac{\sqrt{2}}{2}$=lg$\frac{\sqrt{2}}{2}$.
∴数列{an}是以2为首项,以lg$\frac{\sqrt{2}}{2}$为公差的等差数列.
点评 本题考查了对数的运算性质,等差数列的判断,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.椭圆$\frac{{x}^{2}}{4}$+y2=1的两个焦点为F1,F2,过F2作垂直于x轴的直线与椭圆相交,一个交点为P,则|PF1|等于( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 4 |
12.若a>0,则函数y=ax-1+1的图象经过定点( )
| A. | (1,2) | B. | (2,1) | C. | (0,1+$\frac{1}{a}$) | D. | (2,1+a) |
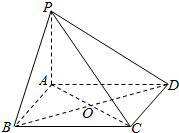 如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.
如图所示,PA垂直于正方形ABCD所在的平面,A为垂足,点O为正方形ABCD对角线AC和BD的交点.