题目内容
13.函数f(x)=cos2x的周期是T,将f(x)的图象向右平移$\frac{T}{4}$个单位长度后得到函数g(x),则g(x)具有性质( )| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递增,为奇函数 | ||
| C. | 在($-\frac{3π}{8}$,$\frac{π}{8}$)上单点递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
分析 利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再根据正弦函数的单调性以及它的图象的对称性,得出结论.
解答 解:函数f(x)=cos2x的周期是T=$\frac{2π}{2}$=π,将f(x)的图象向右平移$\frac{T}{4}$=$\frac{π}{4}$个单位长度后得到函数g(x)=cos2(x-$\frac{π}{4}$)=sin2x的图象,
可得g(x)的最大值为1,当x=$\frac{π}{2}$时,g(x)=0,不是最值,故它的图象不关于直线x=$\frac{π}{2}$对称,故排除A.
g(x)在(0,$\frac{π}{4}$)上单调递增,且g(x)为奇函数,故B正确.
在($-\frac{3π}{8}$,$\frac{π}{8}$)上,2x∈(-$\frac{3π}{4}$,$\frac{π}{4}$),sin2x没有单调性,故g(x)没有单调性,故C错误.
令x=$\frac{3π}{8}$,求得g(x)=sin2x=$\frac{\sqrt{2}}{2}$,不是最值,故g(x)的图象不关于点($\frac{3π}{8}$,0)对称,故D错误,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性以及它的图象的对称性,属于基础题.

练习册系列答案
相关题目
4.若直线y=kx+2k与曲线$y=\sqrt{1-{x^2}}$有两个不同的交点,则k的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
5.函数y=log2(x+2)的定义域是( )
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-2,+∞) | D. | [-2,+∞) |
1.已知函数f(x)=Asin(ωx+φ)$(A>0,|φ|<\frac{π}{2})$的图象(部分)如图所示,则$f(-\frac{1}{2})$=( )
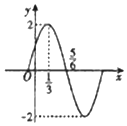

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
5.设偶函数f(x)满足f(x)=2x-4(x≥0),则满足f(a-2)>0的实数a的取值范围为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
1.执行如图所示的程序框图,输出S的值为( )


| A. | 6 | B. | 2log23+1 | C. | 2log23+3 | D. | log23+1 |
1.已知一个平放的各棱长均为 4 的三棱锥内有一个小球,现从该三棱锥顶端向锥内注水,小球慢慢上浮.当注入的水的体积是该三棱锥体积的$\frac{7}{8}$时,小球恰与该三棱锥各侧面及水面相切(小球完全浮在水面上方),则小球的表面积等于( )
| A. | $\frac{7π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |