题目内容
16.空间中点A(2,3,5)与B(3,1,4),则|AB|=$\sqrt{6}$.分析 直接利用空间两点间的距离公式求解即可.
解答 解:∵A(2,3,5),B(3,1,4),
∴|AB|=$\sqrt{{(2-3)}^{2}+{(3-1)}^{2}+{(5-4)}^{2}}$=$\sqrt{6}$,
故答案为$\sqrt{6}$.
点评 本题考查空间两点间的距离公式的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
11.下列各组空间向量相互垂直的是( )
| A. | $\overrightarrow{a}$=(0,1,-1),$\overrightarrow{b}$=(1,0,-1) | B. | $\overrightarrow{a}$=(1,-1,1),$\overrightarrow{b}$=(-1,0,1) | ||
| C. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(0,-2,2) | D. | $\overrightarrow{a}$=(1,-1,1),$\overrightarrow{b}$=(-1,1,-1) |
8.p:?x0∈R,x${\;}_{0}^{2}$+m≤0,q:?x∈R,x2+mx+1>0,如果p,q都是命题且(¬p)∨q为假命题,则实数m的取值范围是( )
| A. | m≤-2 | B. | -2≤m≤0 | C. | 0≤m≤2 | D. | m≥2 |
4.若直线y=kx+2k与曲线$y=\sqrt{1-{x^2}}$有两个不同的交点,则k的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
5.函数y=log2(x+2)的定义域是( )
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-2,+∞) | D. | [-2,+∞) |
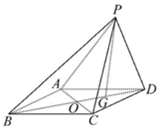 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.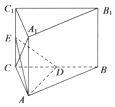 已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.
已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.