题目内容
18.设△ABC内角A,B,C所对的边分别为a,b,c,且a=bcosC+$\sqrt{3}$csinB.(1)若a2sinC=4$\sqrt{3}$sinA,求△ABC的面积;
(2)若a=2$\sqrt{3}$,b=$\sqrt{7}$,且c>b,BC边的中点为D,求AD的长.
分析 (1)已知等式利用正弦定理化简,再利用两角和与差的正弦函数公式及诱导公式变形,求出tanB的值,由B为内角,利用特殊角的三角函数值可求出B的度数,由正弦定理化简已知可得ac的值,利用三角形面积公式即可得解.
(2)由余弦定理整理可得:c2-6c+5=0,从而解得c的值,在△ABD中,由余弦定理即可求得AD的值.
解答 解:(1)∵a=bcosC+$\sqrt{3}$csinB.
∴由正弦定理得:sinA=sinBcosC+$\sqrt{3}$sinBsinC①,
∵sinA=sin(B+C)=sinBcosC+cosBsinC②,
∴$\sqrt{3}$sinB=cosB,即tanB=$\frac{\sqrt{3}}{3}$,
∵B为三角形的内角,
∴B=$\frac{π}{6}$,
∵a2sinC=4$\sqrt{3}$sinA,由正弦定理可得:a2c=4$\sqrt{3}$a,可得:ac=4$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}×4\sqrt{3}×\frac{1}{2}$=$\sqrt{3}$.
(2)∵由(1)可得:B=$\frac{π}{6}$,又a=2$\sqrt{3}$,b=$\sqrt{7}$,
∴由余弦定理b2=a2+c2-2accosB,可得:7=c2+12-2×$2\sqrt{3}×c×\frac{\sqrt{3}}{2}$,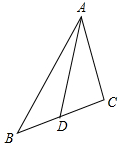
整理可得:c2-6c+5=0,
∴解得:c=5,或1(由c>b,舍去),
∵BC边的中点为D,
∴在△ABD中,由余弦定理可得:
AD=$\sqrt{A{B}^{2}+B{D}^{2}-2AB•BD•cosB}$=$\sqrt{25+3-2×5×\sqrt{3}×\frac{\sqrt{3}}{2}}$=$\sqrt{13}$.
点评 此题考查了正弦定理,余弦定理,三角形面积公式,两角和与差的正弦函数公式在解三角形中的应用,熟练掌握定理及公式是解本题的关键,属于中档题.

| A. | 196 | B. | 224 | C. | 28$\sqrt{7}$ | D. | 28$\sqrt{2}$ |
| A. | -20i | B. | 3i | C. | 20 | D. | 3 |