题目内容

7．在等比数列{an}中，a1+a2+a3+a4+a5=4，a6+a7+a8+a9+a10=28，则a11+a12+…+a15等于（　　）
A．196B．224C．28$\sqrt{7}$D．28$\sqrt{2}$

分析 根据等比数列的性质求出公比即可．

解答 解：∵a1+a2+a3+a4+a5=4，a6+a7+a8+a9+a10=28，
∴（a1+a2+a3+a4+a5）q5=a6+a7+a8+a9+a10，
即4q5=28，即q5=7，
则a11+a12+a13+a14+a15=（a6+a7+a8+a9+a10）q5=28×7=196，
故选：A．

点评 本题主要考查等比数列的性质的应用，根据条件求出公比是解决本题的关键．

练习册系列答案
相关题目
17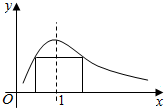．一矩形的一边在x轴上，另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$（x＞0）的图象上，如图，则此矩形绕x轴旋转而成的几何体的体积的最大值是（　　）
A．πB．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{2}$
18．设△ABC内角A，B，C所对的边分别为a，b，c，且a=bcosC+$\sqrt{3}$csinB．
（1）若a2sinC=4$\sqrt{3}$sinA，求△ABC的面积；
（2）若a=2$\sqrt{3}$，b=$\sqrt{7}$，且c＞b，BC边的中点为D，求AD的长．
15．三角形ABC的三个内角A，B，C成等差数列，AC=3，cosC=$\frac{\sqrt{6}}{3}$，则AB=（　　）
A．2$\sqrt{2}$B．8C．2D．4
2．已知sinα=$\frac{3}{5}$，α∈（$\frac{π}{2}$，$\frac{3π}{2}$），求secα-tanα
12．若数列{an}中，a1=1，a2=3，a3=2，an+2=an+1-an，则S2015=2．
19．若a+b=8（a、b＞0），求ab的最大值．
16．已知数列{Cn}，其中Cn=2n+3n．
（1）数列{Cn}是否为等比数列？证明你的结论；
（2）若{Cn+1-pCn}为等比数列，求实数p．
5．已知椭圆C2过椭圆C1：$\frac{{x}^{2}}{14}+\frac{{y}^{2}}{9}=1$的两个焦点和短轴的两个端点，则椭圆C2的离心率为（　　）
A．$\frac{2}{3}$B．$\frac{\sqrt{2}}{2}$C．$\frac{1}{2}$D．$\frac{1}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网