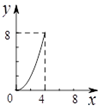
题目内容
6.已知两条直线l1:(a-1)x+2y+1=0,l2:x+ay+1=0,求满足下列条件的a值:(1)l1∥l2
(2)l1⊥l2.
分析 (1)根据两直线平行关系,得$\frac{a-1}{1}=\frac{2}{a}≠1$,即可求出a的值.
(2)根据两直线垂直的关系,即(a-1)+2a=0,即可求出a的值.
解答 解:(1)由题意,$\frac{a-1}{1}=\frac{2}{a}≠1$,∴a=-1;
(2)∵(a-1)+2a=0,∴a=$\frac{1}{3}$.
点评 本题考查两直线平行的性质,两直线垂直的性质,比较基础.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
14.下列有关命题的说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 命题“?x∈R,x2+2x-1<0”的否定是“?x∈R,x2+2x-1>0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 若“p或q”为真命题,则p,q至少有一个为真命题 |
18.已知集合A={x|log2x<1},B={y|y=2x,x≥0},则A∩B=( )
| A. | ∅ | B. | {x|1<x<2} | C. | {x|1≤x<2} | D. | {x|1<x≤2} |
15.在n元数集S={a1,a2,…,an}中,设x(S)=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$,若S的非空子集A满足x(A)=x(S),则称A是集合S的一个“平均子集”,并记数集S的k元“平均子集”的个数为fs(k).已知集合S={1,2,3,4,5,6,7,8,9},T={-4,-3,-2,-1,0,1,2,3,4},则下列说法错误的是( )
| A. | fs(9)=fT(1) | B. | fs(8)=fT(1) | C. | fs(6)=fT(4) | D. | fs(5)=fT(4) |
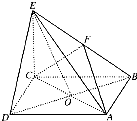 四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.
四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.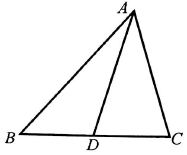 已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.
已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0. 如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.