Question

10．已知P（x₀，y₀）是椭圆C：$\frac{x^2}{4}+{y^2}=1$上的一点，F₁，F₂是C的两个焦点，若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}＜0$，则x₀的取值范围是（　　）

• A． $（{-\frac{{2\sqrt{6}}}{3}，\frac{{2\sqrt{6}}}{3}}）$
• B． $（{-\frac{{2\sqrt{3}}}{3}，\frac{{2\sqrt{3}}}{3}}）$
• C． $（{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$
• D． $（{-\frac{{\sqrt{6}}}{3}，\frac{{\sqrt{6}}}{3}}）$

Answer 1

分析 设以O为原点、半焦距c=$\sqrt{3}$为半径的圆x²+y²=3与椭圆交于A，B两点；由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=3}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$，x=$±\frac{2\sqrt{6}}{3}$
可得x₀的取值范围是（-$-\frac{2\sqrt{6}}{3}，\frac{2\sqrt{6}}{3}$）．

解答 解：如图，设以O为原点、半焦距c=$\sqrt{3}$为半径的圆x²+y²=3与椭圆交于A，B两点；
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=3}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$得${x}^{2}=\frac{8}{3}$，x=$±\frac{2\sqrt{6}}{3}$
要使$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}＜0$，则点P在A、B之间，∴x₀的取值范围是（$-\frac{2\sqrt{6}}{3}，\frac{2\sqrt{6}}{3}$）．
故选：A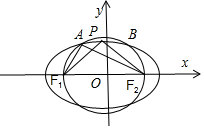

点评 本题考查了椭圆的方程、性质，向量的数量积的运算，属于中档题．