题目内容
11．已知集合A={x|log2（x-1）＜1}，B={x|x2-2x-3＜0}，则“x∈A”是“x∈B”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 分别求出关于集合A、B的不等式，结合集合的包含关系判断即可．
解答 解：∵A={x|log2（x-1）＜1}=（1，3），
B={x|x2-2x-3＜0}=（-1，3），
∴A?B，
∴“x∈A”是“x∈B”的充分不必要条件，
故选：A．
点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．
练习册系列答案
相关题目
1．已知随机变量X满足D（X）=3，则D（3X+2）=（ ）
| A． | 2 | B． | 27 | C． | 18 | D． | 20 |
已知f（x）为定义在R上的奇函数，且当x＞0时，f（x）=x2-4．
一个四棱锥的三视图如图所示，其中侧视图为正三角形，则该四棱锥的体积是$\frac{\sqrt{3}}{6}$，该四棱锥的最长棱的棱长为$\sqrt{2}$．
6．某几何体的三视图如图所示，则该三视图的体积为（ ）
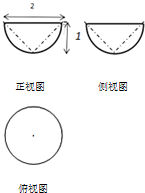
| A． | $\frac{π}{3}$ | B． | $\frac{4}{3}$π | C． | 2π | D． | $\frac{8}{3}$π |
16．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1（a＞0）的一条渐近线为$\sqrt{3}$x+y=0，则a=（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
3．△ABC中，角A，B，C的对边分别是a，b，c，已知a=b，c2=2b2（1-sinC），则C=（ ）
| A． | $\frac{3π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |