题目内容
已知椭圆
+
=1(a>b>0)的右焦点为F(1,0),离心率e=
,A,B是椭圆上的动点.
(Ⅰ)求椭圆标准方程;
(Ⅱ)若直线OA与OB的斜率乘积kOA•kOB=-
,动点P满足
=
+λ
,(其中实数λ为常数).问是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值?若存在,求F1,F2的坐标,若不存在,说明理由;
(Ⅲ)若点A在第一象限,且点A,B关于原点对称,点A在x轴上的射影为C,连接BC并延长交椭圆于点D.证明:AB⊥AD.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆标准方程;
(Ⅱ)若直线OA与OB的斜率乘积kOA•kOB=-
| 1 |
| 2 |
| OP |
| OA |
| OB |
(Ⅲ)若点A在第一象限,且点A,B关于原点对称,点A在x轴上的射影为C,连接BC并延长交椭圆于点D.证明:AB⊥AD.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)利用椭圆的离心率计算公式和b2=a2-c2即可得出;
(Ⅱ)利用向量的坐标运算、点在椭圆上满足椭圆的方程、斜率计算公式及其椭圆的定义即可得出;
(Ⅲ)利用对称的知识、斜率计算公式及其点A,D在椭圆上,只要证明kAB•kAD=-1,即可得出.
(Ⅱ)利用向量的坐标运算、点在椭圆上满足椭圆的方程、斜率计算公式及其椭圆的定义即可得出;
(Ⅲ)利用对称的知识、斜率计算公式及其点A,D在椭圆上,只要证明kAB•kAD=-1,即可得出.
解答:
解:(Ⅰ)由题意可知:
,解得a=
,
∴b2=a2-c2=1,
∴椭圆标准方程为
+y2=1.
(Ⅱ)设P(x,y),A(x1,y1),B(x2,y2),
则由
=
+λ
得
(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2.
∵点A、B在椭圆x2+2y2=2上,
∴x12+2y12=2,x22+2y22=2,
故x2+2y2=(x12+λ2x22+2λx1x2)+2(y12+λ2y22+2λy1y2)
=(x12+2y12)+λ2(x22+2y22)+2λ(x1x2+2y1y2)
=2+2λ2+2λ(x1x2+2y1y2).
∵kOA•kOB=
•
=-
,
∴x1x2+2y1y2=0,
∴x2+2y2=2+2λ2.即
+
=1.
∴P点是椭圆
+
=1上的点,
设该椭圆的左、右焦点为F1,F2,
由椭圆的定义可知:|PF1|+|PF2|为定值.
又∵c=
,
∴此椭圆的两焦点的坐标为F1(-
,0),F2(
,0).
∴存在两个定点F1(-
,0),F2(
,0).使得|PF1|+|PF2|=2
.
(Ⅲ)证明:设A(x1,y1),D(x2,y2),
由题设可知:x1>0,x2>0,y1>0,y2>0,x1≠x2,C(x1,0),B(-x1,-y1).
由题意可知:kCB=kBD,∴
=
③
kAB•kAD+1=
•
+1④
将③代入④可得:kAB•kAD+1=
•
+1=
⑤
点A,D在椭圆x2+2y2=2上,
∴kAB•kAD+1=
=
=0.
∴kAB•kAD=-1,
∴AB⊥AD.
|
| 2 |
∴b2=a2-c2=1,
∴椭圆标准方程为
| x2 |
| 2 |
(Ⅱ)设P(x,y),A(x1,y1),B(x2,y2),
则由
| OP |
| OA |
| OB |
(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2.
∵点A、B在椭圆x2+2y2=2上,
∴x12+2y12=2,x22+2y22=2,
故x2+2y2=(x12+λ2x22+2λx1x2)+2(y12+λ2y22+2λy1y2)
=(x12+2y12)+λ2(x22+2y22)+2λ(x1x2+2y1y2)
=2+2λ2+2λ(x1x2+2y1y2).
∵kOA•kOB=
| y1 |
| x1 |
| y2 |
| x2 |
| 1 |
| 2 |
∴x1x2+2y1y2=0,
∴x2+2y2=2+2λ2.即
| x2 |
| 2+2λ2 |
| y2 |
| 1+λ2 |
∴P点是椭圆
| x2 |
| 2+2λ2 |
| y2 |
| 1+λ2 |
设该椭圆的左、右焦点为F1,F2,
由椭圆的定义可知:|PF1|+|PF2|为定值.
又∵c=
| 1+λ2 |
∴此椭圆的两焦点的坐标为F1(-
| 1+λ2 |
| 1+λ2 |
∴存在两个定点F1(-
| 1+λ2 |
| 1+λ2 |
| 2+2λ2 |
(Ⅲ)证明:设A(x1,y1),D(x2,y2),
由题设可知:x1>0,x2>0,y1>0,y2>0,x1≠x2,C(x1,0),B(-x1,-y1).
由题意可知:kCB=kBD,∴
| y1 |
| 2x1 |
| y2+y1 |
| x2+x1 |
kAB•kAD+1=
| y1 |
| x1 |
| y2-y1 |
| x2-x1 |
将③代入④可得:kAB•kAD+1=
| 2(y2+y1) |
| x2+x1 |
| y2-y1 |
| x2-x1 |
(
| ||||||||
|
点A,D在椭圆x2+2y2=2上,
∴kAB•kAD+1=
(
| ||||||||
|
| 2-2 | ||||
|
∴kAB•kAD=-1,
∴AB⊥AD.
点评:本题综合考查了椭圆的标准方程及其性质、点在椭圆上可知满足椭圆的方程、斜率计算公式、对称的性质、直线垂直与斜率的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
在区间[0,4]内随机取两个实数a,b,则使得方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
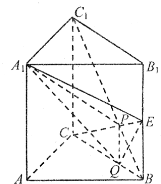 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=
如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=