题目内容
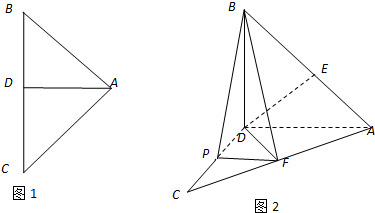
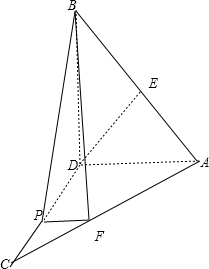
如图1,AD是直角△ABC斜边上的高,沿AD把△ABC的两部分折成直二面角(如图2),DF⊥AC于F.
(Ⅰ)证明:BF⊥AC;
(Ⅱ)设∠DCF=θ,AB与平面BDF所成的角为α,二面角B-FA-D的大小为β,试用tanθ,cosβ表示tanα;
(Ⅲ)设AB=AC,E为AB的中点,在线段DC上是否存在一点P,使得DE∥平面PBF?若存在,求
的值;若不存在,请说明理由.
(Ⅰ)证明:BF⊥AC;
(Ⅱ)设∠DCF=θ,AB与平面BDF所成的角为α,二面角B-FA-D的大小为β,试用tanθ,cosβ表示tanα;
(Ⅲ)设AB=AC,E为AB的中点,在线段DC上是否存在一点P,使得DE∥平面PBF?若存在,求
| DP |
| PC |

考点:直线与平面垂直的性质,直线与平面平行的判定
专题:三角函数的求值,空间位置关系与距离,空间角
分析:(1)首先利用折叠,把平面问题转化成空间问题,进一步利用面面垂直转化成线面垂直和线线垂直.
(2)利用三角函数及定义建立等量关系
(3)存在性问题的确定,先确定结论,然后进行证明,进一步得出结论.
(2)利用三角函数及定义建立等量关系
(3)存在性问题的确定,先确定结论,然后进行证明,进一步得出结论.
解答:
 证明:(Ⅰ)∵AD⊥DB,AD⊥DC,
证明:(Ⅰ)∵AD⊥DB,AD⊥DC,
∴∠BDC是二面角B-DA-C的平面角.
又∵二面角B-DA-C是直二面角,
∴BD⊥DC,
∴BD⊥平面ADC,
∴BD⊥AC,
又DF⊥AC,∴AC⊥平面BDF,∴BF⊥AC.
解:(Ⅱ)由(Ⅰ)∠ABF=α⇒tanα=
,
∠BFD=β⇒cosβ=
.
利用三角形相似得:∠ADF=∠DCF=θ⇒tanθ=
,
∴tanθcosβ=
=tanα.
解:(Ⅲ)存在
=
,使DE∥平面PBF
理由:连接CE交BF于点M,连接PM,则PM∥DE.
∵AB=AC,∴AD=DC,
∴F为AC的中点,而E为AB的中点,
∴M为△ABC的重心,
∴
=
,∴
=
.
即在线段DC上存在一点P,此时
=
,使DE∥平面PBF.
故答案为:(1)略
(2)tanθcosβ=tanα
(3)存在
=
,使DE∥平面PBF
 证明:(Ⅰ)∵AD⊥DB,AD⊥DC,
证明:(Ⅰ)∵AD⊥DB,AD⊥DC,∴∠BDC是二面角B-DA-C的平面角.
又∵二面角B-DA-C是直二面角,
∴BD⊥DC,
∴BD⊥平面ADC,
∴BD⊥AC,
又DF⊥AC,∴AC⊥平面BDF,∴BF⊥AC.
解:(Ⅱ)由(Ⅰ)∠ABF=α⇒tanα=
| AF |
| BF |
∠BFD=β⇒cosβ=
| DF |
| BF |
利用三角形相似得:∠ADF=∠DCF=θ⇒tanθ=
| AF |
| DF |
∴tanθcosβ=
| AF |
| BF |
解:(Ⅲ)存在
| DP |
| PC |
| 1 |
| 2 |
理由:连接CE交BF于点M,连接PM,则PM∥DE.
∵AB=AC,∴AD=DC,
∴F为AC的中点,而E为AB的中点,
∴M为△ABC的重心,
∴
| EM |
| MC |
| 1 |
| 2 |
| DP |
| PC |
| 1 |
| 2 |
即在线段DC上存在一点P,此时
| DP |
| PC |
| 1 |
| 2 |
故答案为:(1)略
(2)tanθcosβ=tanα
(3)存在
| DP |
| PC |
| 1 |
| 2 |
点评:本题考查的知识要点:面面垂直的性质定理与线面垂直和线线垂直的转化,三角函数只是在三角形中的应用,直二面角的应用,存在性问题的确定与证明方法.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
“m=1”是“直线x+m2y=0与直线x-y=1垂直”的( )
| A、充要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
若∠AOB=∠A1O1B1且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是( )
| A、OB∥O1B1且方向相同 |
| B、OB∥O1B1 |
| C、OB与O1B1不平行 |
| D、OB与O1B1不一定平行 |
不等式组
表示的平面区域为M,若直线y=kx-3k与平面区域M有公共点,则k取值范围是( )
|
A、(0,
| ||
B、(-∞,
| ||
C、[-
| ||
D、(-∞,
|