题目内容
12．集合A={x∈N|x≤6}，B={x∈R||2-x|＞2}，则A∩B=（ ）| A． | {0，5，6} | B． | {5，6} | C． | {4，6} | D． | {x|4＜x≤6} |
分析 先化简集合A、B，再求出A∩B的值．
解答 解：集合A={x∈N|x≤6}={0，1，2，3，4，5，6}，
B={x∈R||2-x|＞2}={x∈R|x＜0或x＞4}，
所以A∩B={5，6}．
故选：B．
点评 本题考查了集合的化简与运算问题，是基础题目．
练习册系列答案
相关题目
3．已知全集U=R，若A={y|y=2x，x≤0}，则∁RA=（ ）
| A． | （-∞，0]∪（1，+∞） | B． | （1，+∞） | C． | （-∞，0）∪[1，+∞） | D． | （-∞，0） |
20．某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些这些学生的原始成绩均分布在[50，100]内，发布成绩使用等级制，各等级划分标准见表，规定：A，B，C三级为合格等级，D为不合格等级．
为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图所示，样本中分数在80分及以上的所有数据的茎叶图如图所示．
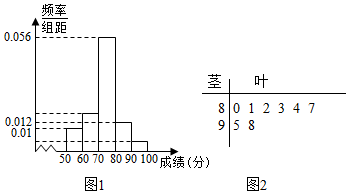
（1）求n和频率分布直方图中的x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率；
（3）在选取的样本中，从A，C两个等级的学生中随机抽取了3名学生进行调研，记ξ表示抽取的3名学生中为C等级的学生人数，求随机变量ξ的分布列及数学期望．
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
（1）求n和频率分布直方图中的x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率；
（3）在选取的样本中，从A，C两个等级的学生中随机抽取了3名学生进行调研，记ξ表示抽取的3名学生中为C等级的学生人数，求随机变量ξ的分布列及数学期望．
7．已知集合M={x|x2＞1}，N={-2，-1，0，1，2}，则M∩N=（ ）
| A． | {0} | B． | {2} | C． | {-2，-1，1，2} | D． | {-2，2} |
在某次考试中，从甲、乙两个班各抽取10名学生的数学成绩进行统计分析，两个班成绩的茎叶图如图所示，成绩不小于90分的为及格．
4．若复数$z=\frac{1-3i}{1+i}$，则|z+1|=（ ）
| A． | 3 | B． | 2 | C． | $\sqrt{2}$ | D． | $\sqrt{5}$ |
2．我国延迟退休年龄将借鉴国外经验，拟对不同群体采取差别措施，并以“小步慢走”的方式实施．现对某市工薪阶层关于“延迟退休年龄”的态度进行调查，随机抽取了50人，他们月收入的频数分布及对“延迟退休年龄”反对的人数如下表．
（Ⅰ）由以上统计数据估算月收入高于5500的调查对象中，持反对态度的概率；
（Ⅱ）若对月收入在[1500，2500），[2500，3500）的被调查对象中各随机选取两人进行跟踪调查，记选中的4人中赞成“延迟退休年龄”的人数为ξ，求随机变量ξ的分布列和数学期望．
| 月收入（元） | [1500，2500） | [2500，3500） | [3500，4500） | [4500，5500） | [5500，6500） | [6500，7500） |
| 频数 | 5 | 10 | 14 | 11 | 6 | 4 |
| 反对人数 | 4 | 8 | 11 | 6 | 2 | 1 |
（Ⅱ）若对月收入在[1500，2500），[2500，3500）的被调查对象中各随机选取两人进行跟踪调查，记选中的4人中赞成“延迟退休年龄”的人数为ξ，求随机变量ξ的分布列和数学期望．