题目内容
12.已知x,y满足不等式组$\left\{\begin{array}{l}{x-3y+2≥0}\\{x+y-6≤0}\\{y≥1}\end{array}\right.$,若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的取值范围是[$\frac{1}{8}$,$\frac{2}{7}$].分析 作出可行域,根据可行域和最优解的个数得出a的值,利用$\frac{y}{x-a}$的几何意义得出答案.
解答 解:作出约束条件表示的可行域如图: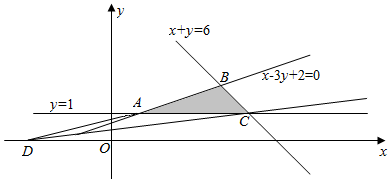
当a=0时,显然z=x+ay只有一个最优解,不符合题意,
当a>0时,由z=x+ay得y=-$\frac{1}{a}x$+$\frac{z}{a}$,
∴当直线y=-$\frac{1}{a}x$+$\frac{z}{a}$经过点A时截距最小,即z最小,
显然最优解只有一个,不符合题意.
当a<0时,由z=x+ay得y=-$\frac{1}{a}x$+$\frac{z}{a}$,
∵z=x+ay取得最小值的最优解有无数个,
∴当直线y=-$\frac{1}{a}x$+$\frac{z}{a}$与直线AB:x-3y+2=0重合时,截距最大,即z最小.
∴a=-3.
设D(-3,0),k=$\frac{y}{y-a}=\frac{y}{x+3}$,
解方程组$\left\{\begin{array}{l}{x+y=6}\\{y=1}\end{array}\right.$得C(5,1).解方程组$\left\{\begin{array}{l}{x+y-6=0}\\{x-3y+2=0}\end{array}\right.$得B(4,2).
∴kCD=$\frac{1-0}{5+3}$=$\frac{1}{8}$,kBD=$\frac{2-0}{4+3}$=$\frac{2}{7}$.
∴$\frac{1}{8}$≤k≤$\frac{2}{7}$.
故答案为[$\frac{1}{8}$,$\frac{2}{7}$].
点评 本题考查了简单的线性规划,根据可行域得出a的值是解题关键.

练习册系列答案
相关题目
3.已知A为△ABC的最小内角,若向量$\overrightarrow{a}$=(cosA,1),$\overrightarrow{b}$=(2sin(A+$\frac{π}{6}$),1),则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是( )
| A. | [-$\frac{1}{2}$,$\frac{5}{2}$] | B. | (-$\frac{1}{2}$,$\frac{5}{2}$] | C. | [2,$\frac{5}{2}$] | D. | (2,$\frac{5}{2}$] |
17.某校为了了解一次数学质量检测的情况,随机抽取了100名学生的成绩,并按如表的分数段计数:
则本次检测中所抽取样品的平均成绩为89.5.
| 分数段 | (0,80) | [80,110) | [110,150) |
| 频数 | 35 | 50 | 15 |
| 平均成绩 | 60 | 98 | 130 |
11.已知抛物线y2=8x的准线过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为( )
| A. | x2+$\frac{{y}^{2}}{3}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | y2+$\frac{{x}^{2}}{3}$=1 | D. | y2-$\frac{{x}^{2}}{3}$=1 |
12.集合A={x∈N|x≤6},B={x∈R||2-x|>2},则A∩B=( )
| A. | {0,5,6} | B. | {5,6} | C. | {4,6} | D. | {x|4<x≤6} |