题目内容
17. 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.(Ⅰ)用样本估计总体,请根据茎叶图对甲、乙两个班级的成绩进行比较;
(Ⅱ)在甲、乙两班成绩及格的同学中再随机抽出2名同学的试卷做分析,求抽出的2人恰好都是甲班学生的概率.
分析 (Ⅰ)从茎叶图分别求出甲、乙班的平均分和方差,从而得到甲乙两班平均分相同,但是乙班比甲班成绩更集中更稳定.
(Ⅱ)由茎叶图可知,甲班的成绩及格的有95,98,106,108有4人,乙班的成绩及格有91,92,93,95,101有5人,随机抽出2名同学,共有C92=36种,其中全为甲班的有C42=6种,根据概率公式计算即可.
解答 解:(Ⅰ)从茎叶图可以得到:
甲班的平均分为:$\overline{{x}_{甲}}$=$\frac{1}{10}$(72+75+77+84+87+88+95+98+106+108)=89分,
乙班平均分为:$\overline{{x}_{乙}}$=$\frac{1}{10}$(78+79+86+87+88+91+92+93+95+101)=89分.
甲班的方差S甲2=$\frac{1}{10}$[(72-89)2+(75-89)2+(77-89)2+(84-89)2+(87-89)2+(88-89)2+(95-89)2+(98-89)2+(106-89)2+(108-89)2]=142.6,
乙班的方差S乙2=$\frac{1}{10}$[(78-89)2+(79-89)2+(86-89)2+(87-89)2+(88-89)2+(91-89)2+(92-89)2+(93-89)2+(95-89)2+(101-89)2]=44.4,
所以甲乙两班平均分相同,但是乙班比甲班成绩更集中更稳定.
(Ⅱ)由茎叶图可知,甲班的成绩及格的有95,98,106,108有4人,乙班的成绩及格有91,92,93,95,101有5人,
随机抽出2名同学,共有C92=36种,其中全为甲班的有C42=6种,
故抽出的2人恰好都是甲班学生的概率P=$\frac{6}{36}$=$\frac{1}{6}$.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

| 分数段 | (0,80) | [80,110) | [110,150) |
| 频数 | 35 | 50 | 15 |
| 平均成绩 | 60 | 98 | 130 |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | {0,5,6} | B. | {5,6} | C. | {4,6} | D. | {x|4<x≤6} |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | $(\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})$ |
| A. | $1-\frac{1}{e}$ | B. | $\frac{e+1}{e^2}$ | C. | $\frac{1}{e}$ | D. | $\frac{e-1}{e^2}$ |
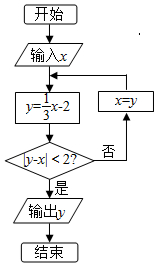 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )| A. | -$\frac{23}{9}$ | B. | 1 | C. | $\frac{8}{9}$ | D. | -$\frac{5}{3}$ |