题目内容
2.我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数如下表.| 月收入(元) | [1500,2500) | [2500,3500) | [3500,4500) | [4500,5500) | [5500,6500) | [6500,7500) |
| 频数 | 5 | 10 | 14 | 11 | 6 | 4 |
| 反对人数 | 4 | 8 | 11 | 6 | 2 | 1 |
(Ⅱ)若对月收入在[1500,2500),[2500,3500)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为ξ,求随机变量ξ的分布列和数学期望.
分析 (1)月收入高于5500的人数有10人,其中持反对态度的人数有3人,由此能估算月收入高于4000的调查对象中,持反对态度的概率.
(2)由已知ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)根据题意,由于对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,
他们月收入的频数分布可知月收入高于5500的人数有6+4=10人,
其中持反对态度的人数有2+1=3人,
∴估算月收入高于4000的调查对象中,持反对态度的概率p=$\frac{3}{10}=0.3$.
(2)根据题意,由于对月收入在[1500,2500),[2500,3500)的被调查对象中各随机选取两人进行跟踪调查,
可知ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{{C}_{4}^{2}}{{C}_{5}^{2}}×\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$=$\frac{28}{75}$,
P(ξ=1)=$\frac{{C}_{1}^{1}{C}_{4}^{1}}{{C}_{5}^{2}}×\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$+$\frac{{C}_{4}^{2}}{{C}_{5}^{2}}×\frac{{C}_{2}^{1}{C}_{8}^{1}}{{C}_{10}^{2}}$=$\frac{104}{225}$,
P(ξ=2)=$\frac{{C}_{1}^{1}{C}_{4}^{1}}{{C}_{5}^{2}}×\frac{{C}_{2}^{1}{C}_{8}^{1}}{{C}_{10}^{2}}$+$\frac{{C}_{4}^{2}}{{C}_{5}^{2}}×\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{7}{45}$
P(ξ=3)=$\frac{{C}_{1}^{1}{C}_{4}^{1}}{{C}_{5}^{2}}×\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{2}{225}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{28}{75}$ | $\frac{104}{225}$ | $\frac{7}{45}$ | $\frac{2}{225}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

| A. | {0,5,6} | B. | {5,6} | C. | {4,6} | D. | {x|4<x≤6} |
| A. | f(sin1)<f(cos1) | B. | f(sin1)=f(cos1) | C. | f(sin1)>f(cos1) | D. | 不确定 |
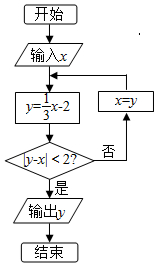 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )| A. | -$\frac{23}{9}$ | B. | 1 | C. | $\frac{8}{9}$ | D. | -$\frac{5}{3}$ |
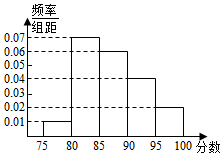 2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕,在田径锦标赛期间需要大量大学生志愿者.志愿者先由相关的学校先进行选拔,合格者方能参加锦标赛组委会的面试.接到任务的某学校对报名的志愿者进行了一次相关知识小测试.现从中随机抽取100名学生的测试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.