题目内容
由曲线y=x2-2x与直线x+y=0所围成的封闭图形的面积为 ．
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：联立方程组求出积分的上限和下限，结合积分的几何意义即可得到结论．
解答：
解：由曲线y=x2-2x与直线x+y=0，得x2-x=0，解得x=0或x=1，
则根据积分的几何意义可知所求的几何面积S=
(-x-x2+2x)dx=(-
x3+
x2)
=
，
故答案为：
．
则根据积分的几何意义可知所求的几何面积S=
| ∫ | 1 0 |
| 1 |
| 3 |
| 1 |
| 2 |
| | | 1 0 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：本题主要考查积分的应用，作出对应的图象，求出积分上限和下限，是解决本题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知sin（
+a）=
，则cos2a的值为（ ）
| π |
| 2 |
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知命题p：复数z=
在复平面内所对应的点位于第四象限；命题q：?x＞0使得2-x=ex，则下列命题中为真命题的是（ ）
| 1+i |
| i |
| A、p∧q |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
设α、β为两个不同的平面，m、n为两条不同的直线，则a⊥b的一个充分条件是（ ）
| A、a⊥α，b∥β，α⊥β |
| B、a⊥α，b⊥β，α∥β |
| C、a?α，b⊥β，α∥β |
| D、a?α，b∥β，α⊥β |
已知数列{an}满足：a1=1，
=
，n∈N*，{an}的前项和为Sn，则（ ）
| 1 |
| an+1 |
| 1 |
| 2an |
A、Sn=2-（
| ||
B、Sn=2-（
| ||
| C、Sn=2n-1 | ||
| D、Sn=2n-1-1 |
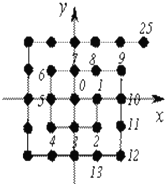将平面直角坐标系中的格点（横、纵坐标均为整数的点）按如下规则标上数字标签：原点处标0，点（1，0）处标1，点（1，-1）处标2，点（0，-1）处标3，点（-1，-1）处标4，…，点（0，1）处标7，…，依此类推，则标签20152的格点的坐标为（ ）| A、（1008，1007） |
| B、（1007，1006） |
| C、（1007，1005） |
| D、（1006，1005） |